Analýza dat v neurologii
XLIX. Vzájemná srovnatelnost a aproximace odhadů relativního rizika a poměru šancí
Autoři:
L. Dušek; T. Pavlík; J. Jarkovský
; J. Koptíková
Působiště autorů:
Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise:
Cesk Slov Neurol N 2015; 78/111(1): 100-102
Kategorie:
Okénko statistika
V minulém díle seriálu jsme otevřeli problematiku tzv. předpokladu vzácného onemocnění (rare disease assumption), jehož uplatněním jsme schopni aproximovat odhad relativního rizika (RR) s pomocí odhadu poměru šancí (OR) získaného v retrospektivní observační studii. Předpokladem zde je, že při vzácném výskytu studovaného jevu se odhady RR a OR numericky přibližují a lze je považovat za numericky srovnatelné. Hlavní přínos je možnost srovnat na bázi hodnot RR již publikované výstupy studií provedených s různým experimentálním plánem (např. odhad RR z kohortových studií s odhady OR ze studií případů a kontrol).
Problém, na který ukázal již příklad v minulém díle, je ale platnost tohoto předpokladu v konkrétní situaci. Předpoklad vzácného onemocnění je totiž jen matematický předpoklad, jehož uplatnitelnost by měla být vždy ověřena. Ačkoli různí autoři poměrně často citují hranici prevalence 10 % a nižší jako dostačující pro platnost tohoto předpokladu, ve skutečnosti nejde v takovém případě o nijak vzácný výskyt jevu. Prevalence 10 % znamená výskyt onemocnění u jednoho člověka z 10 osob, zatímco epidemiologická definice vzácné choroby počítá s výskytem 1 : 2 000. Ve skutečnosti neexistuje žádná exaktně daná hranice pro nezkreslenou aproximaci hodnot RR z odhadu OR, a hranice 10 % má v literatuře velmi mnoho kritiků, zejm. pokud se používá paušálně a bez ověření.
Zde jistě čtenáře napadne legitimní otázka, jak si tedy má výzkumník nematematik ověřit platnost předpokladu vzácného onemocnění v konkrétní situaci? Odpověď je naštěstí jednoduchá, neboť toto ověření je možné i bez složitých matematických postupů. Stačí vyjít ze vstupních údajů, které při srovnání různých studií musí být známy. Představme si publikaci běžné studie případů a kontrol, kde její čtenář vždy zná:
- primární tabulku četností (kvalitní publikovaná studie musí uvádět velikost vzorku, resp. počet analyzovaných subjektů, osob),
- hodnotu prevalence znaku ve skupině případů i kontrol (tím je myšlen odhad prevalence získaný na konkrétním vzorku studie, vypočítaný z tabulky četností),
- výsledný odhad hodnoty OR.
Tyto údaje jsou dostačující pro ověření platnosti předpokladu vzácného onemocnění. Aproximace hodnoty RR z takto publikovaného odhadu OR neznamená nic jiného než předpoklad, že daný odhad OR je v dané situaci numericky blízký až totožný s hodnotou RR. A tedy, že platí vztah OR/ RR ≈ 1. Známe‑li vstupní tabulku četností, nic nám nebrání v dané situaci pokusně vypočítat i hodnotu RR a posoudit tak, zda je aproximace možná, respektive vhodná.
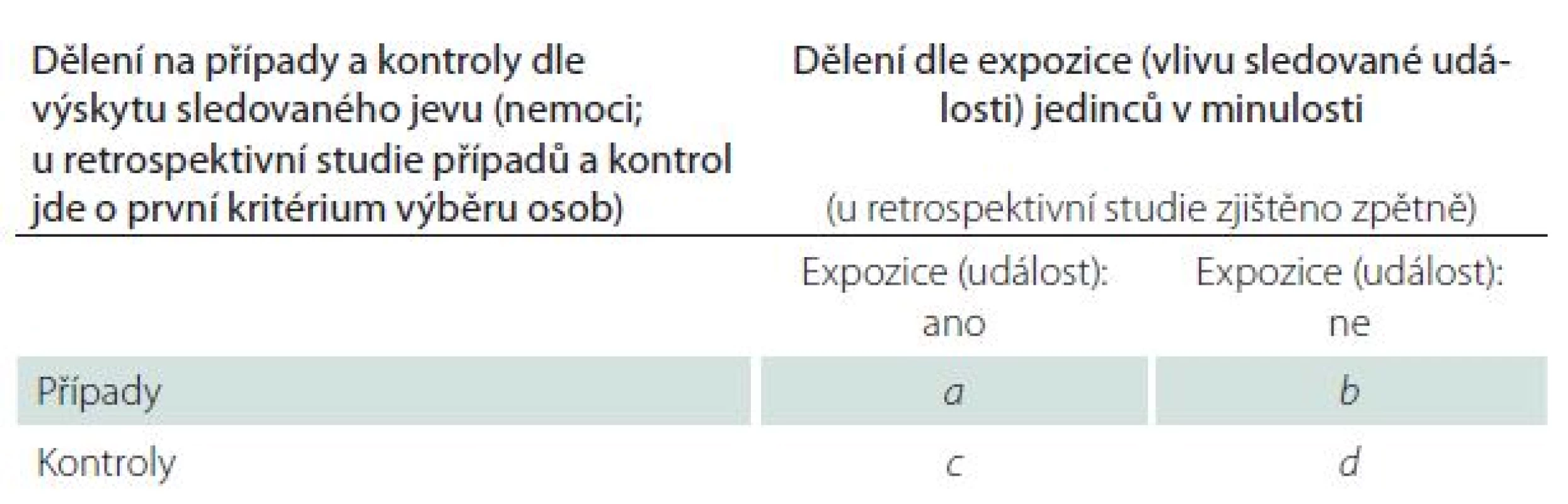
Připomeňme si nejjednodušší tabulku četností 2 × 2 s typickým značením četností v jednotlivých polích a, b, c, d (tab. 1).Při velmi vzácném výskytu jevu budou četnosti v polích a, b tabulky velmi malé a výpočet hodnoty RR se bude přibližně rovnat vztahu: RR ≈ [a/ c]/ [b/ d] ≈ a*d/ b*c ≈ OR. Stejný jev můžeme vysvětlit i pomocí definičního vztahu pro šanci (O), kterou například pro rizikový jev A definujeme takto: OA = PA/ (1 – PA),kde PA je pravděpodobnost nastání jevu A,neboli zde riziko jevu A. Pokud je jev A vzácný, pak je PA velmi malé číslo a platí, že OA ≈ PA. V takovém případě lze tedy na základě hodnoty šance aproximovat pravděpodobnost nastání jevu, a tudíž odhad poměru šancí umožňuje aproximovat hodnotu relativního rizika.
Z tohoto pohledu vypadá verifikace předpokladu vzácného onemocnění relativně snadně, neboť jeho platnost se jeví jako závislá především na relativním výskytu případů mezi exponovanými a neexponovanými jedinci. Realita je ale bohužel složitější a kromě vlastní prevalence onemocnění je vztah mezi RR a OR ovlivněn i absolutní hodnotou relativního rizika a poměru šancí v dané studii. Právě proto je verifikace předpokladu v konkrétní situaci důležitá, neboť zvláště u vyšších hodnot OR nemusí být i při relativně nízké prevalenci aproximace na RR obhajitelná.

Tento fakt dokumentuje příklad 1, který výše uvedené ověření vztahu OR ≈ RR shrnuje na různých výstupech modelových studií. Z příkladu je patrné, že:
- při znalosti primárních dat experimentu můžeme současně snadno vypočítat hodnotu OR i RR a ověření předpokladu vzácného onemocnění je tak dostupné i matematickým neprofesionálům;
- vztah OR a RR si lze lehce modelově ověřovat na různých vymyšlených příkladech simulujících experimentální situace;
- zvláště obezřetní musíme být v situaci, kdy je prevalence znaku relativně vysoká (3 % a vyšší) a daná retrospektivní studie vedla k odhadu vysoké nebo naopak nízké hodnoty OR (> 2,5; < 0,5);
- při neplatnosti předpokladu vzácného onemocnění poměr šancí neaproximuje dobře odhad relativního rizika; čím je studované onemocnění častější, tím více OR nadhodnocuje RR (při RR > 1) anebo ji více podhodnocuje (při RR < 1).
Srovnatelnost a aproximace různých odhadů OR a RR jsou v současnosti aktuální téma rozebírané v řadě recentních prací (viz literatura uvedená v díle seriálu č. 48). K tomu v nemalé míře přispívá současná renezance observačních studií a také reálný nástup personalizované medicíny. Rostoucí počet prognostických a rizikových markerů, které je nutné respektovat, často znemožňuje efektivní realizaci randomizovaných komparativních studií prostě z toho důvodu, že není možné získat adekvátní počty probandů pro narůstající množství ramen takové studie. Využívání retrospektivních studií tento problém sice částečně řeší, avšak jejich výstupy nemohou kvalitou prospektivní komparativní studie zcela nahradit. Publikované observační výstupy tedy následně vyžadují ve zvýšené míře souhrnné analýzy (metaanalýzy), u kterých se aproximaci odhadů OR na RR často nelze vyhnout.
I proto můžeme v literatuře nalézt návrhy postupů, jak z odhadu poměru šancí korektně usoudit na hodnotu relativního rizika, jež je pro řadu autorů stále lépe interpretovatelnou mírou rizika. Jeden z takových postupů navržený pro kohortové studie publikovali v roce 1998 Zang a Yu. Postup, ve kterém navrhli výpočet hodnoty RR z odhadu OR adjustovaného na vliv zavádějících faktorů, v zjednodušené podobě přibližujeme v příkladu 2. Autoři řeší fakt, že stále častěji využívané metody vedoucí k odhadu OR v prospektivních kohortových studiích (např. logistická regrese) neumožňují korektně usuzovat na hodnotu RR. Navržená metoda korekce OR je cenná i v tom, že umožňuje aproximaci na RR pro běžné jevy s prevalencí > 10 %. Korekce odhadu RR je nutná především v oblasti hodnot OR > 2,5 anebo OR < 0,5. Jakkoli je tento postup lákavý, je třeba jej využívat s obezřetností. Na omezení použití této korekce upozornili ve své reakci na původní návrh autoři McNutt et al v roce 1999. Postup navržený Zangem a Yuem je použitelný pouze u asociačních studií, kde zavádějící faktory nemodifikují účinek, a hodnoty RR jsou stejné ve všech subkohortách daných zavádějícími faktory. Problém ovšem je, jak takovou situaci správně identifikovat a doložit, a proto má postup uvedený v příkladu 2poměrně významná omezení v reálném uplatnění.

Současná literatura a dostupné důkazy se většinou přiklánějí k názoru nepoužívat odhady poměru šancí u studií, které umožňují přímočarý odhad relativního rizika. Tedy zejm. u prospektivních kohortových a průřezových studií. Velmi srozumitelnou formou tento problém rozebírá například Lee, na jehož sdělení roku 1994 uvádíme odkaz v seznamu literatury. Ovšem zdá se, že s chybnou záměnou a interpretací odhadů OR a RR stále bojuje mnoho původních publikací. Podle řady nedávných přehledů literatury je poměr šancí často chybně interpretován jako relativní riziko anebo je relativní riziko nesprávně kalkulováno u retrospektivních studií, kde jej nelze nezkresleně odhadnout. Například Holcomb et al (2001) uvádějí v průzkumu prací ze dvou časopisů více než 25% chybovost v této oblasti. Granados (1995) upozornil na to, že problematická je i definice OR a RR v řadě využívaných matematických a klinických odborných slovníků, které chybně oba ukazatele definují nebo je zaměňují. Potom se ovšem nelze divit tomu, že se chyby kumulují. Držet se jednoduchých pravidel a používat poměr šancí především tam, kde nemůžeme odhadnout relativní riziko (tj. zvláště u retrospektivních observačních studií), je asi nejlepší cesta, jak si při publikaci vlastních dat nezkomplikovat cestu k jejich interpretaci.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
MU, Brno
e‑mail: dusek@iba.muni.cz
Zdroje
1. Granados JA. Odds and odds ratio: an odd confusion. Epidemiology 1995; 6(5): 571– 572.
2. Holcomb WL jr, Chaiworapongsa T, Luke DA, Burgdorf KD. An odd measure of risk: use and misuse of the odds ratio. Obstet Gynecol 2001; 98(4): 685– 688.
3. Lee J. Odds ratio or relative risk for cross‑ sectional data? Int J Epidemiology 1994; 23(1): 201– 203.
4. McNutt LA, Hafner JP, Xue X. Correcting the odds ratio in cohort studies of common outcomes. JAMA 1999; 282(6): 529.
5. Zhang J, Yu KF. What‘s the relative risk? A method of correcting the odds ratio in cohort studies of common outcomes. JAMA 1998; 280(19): 1690– 1691.
Štítky
Dětská neurologie Neurochirurgie NeurologieČlánek vyšel v časopise
Česká a slovenská neurologie a neurochirurgie

2015 Číslo 1
Nejčtenější v tomto čísle
- Protokol diagnostiky a léčby hyponatremie a hypernatremie v neurointenzivní péči
- Mini‑Mental State Examination – česká normativní studie
- Autoimunitní encefalitidy
- Asymptomatická spondylogenní komprese krční míchy
