Analýza dat v neurologii.
V. Přínos a důsledky transformace dat
Autoři:
L. Dušek; T. Pavlík; J. Koptíková
Působiště autorů:
Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise:
Cesk Slov Neurol N 2007; 70/103(5): 600-603
Kategorie:
Okénko statistika
Úvod
Tato kapitola statistického seriálu rozšiřuje předchozí díly věnované sumárním statistikám a prezentaci opakovaně měřených hodnot. Pojem, kterým se budeme zabývat, se jmenuje transformace dat nebo lépe statická transformace dat. Zadáte-li si do internetového vyhledavače pojem data transformation, budete ve většině odkazů poučeni, že jde o konverzi dat z jednoho formátu do jiného. Heslo vás tedy bude odvádět spíše na pole aplikované informatiky. Při zpracování dat definujeme transformaci v užším slova smyslu – jde o aplikaci matematické funkce na primární data za účelem jejich převedení do podoby výhodnější pro zpracování požadovanými statistickými metodami. Nejčastějším požadavkem je dosažení symetrického tvaru rozložení, tedy tzv. normálního typu, a proto je velká část transformací označována jako normalizace hodnot. Důvodů pro transformaci dat je ovšem více než pouze dosažení normálního tvaru rozložení a obecně je lze sumarizovat takto:
- vyřešení asymetrického nebo atypického tvaru rozložení
- vyrovnání variability hodnot v různých srovnávaných skupinách
- řešení velkého numerického rozsahu hodnot, který komplikuje následné zpracování a snižuje přehlednost výstupů
- potřeba přehledného grafického znázornění dat
- linearizace nebo jiná úprava vztahu dvou a více proměnných
Výpočetní stránka je jednoduchá. Vybranou matematickou funkci aplikujeme na každou jednotlivou hodnotu v souboru a tzv. primární data takto změníme na data transformovaná a na nich potom provedeme potřebné statistické operace (sumarizaci dat, statistické testy, srovnání skupin apod). Celý proces ovšem musíme mít pod kontrolou, což znamená především následující:
- Ne všechny funkce jsou vhodné na všechny typy dat. Po transformaci tedy musíme nejprve prověřit, zda jsme skutečně dosáhli potřebného efektu.
- Proces musí být plně vratný. Transformovaná data tedy musíme být schopni konvertovat zpět na primární hodnoty.
Transformace dat je užitečný nástroj, který může podstatně zjednodušit řadu problémů souvisejících s reálnými daty. Nejčastěji jde o nejrůznější variace následujících problémů:
- Sledujeme například růst nějakého biologického systému nebo vývoj jeho funkcí v čase a hodnoty měřeného znaku postupně výrazně numericky rostou. Tím vznikají při zpracování velké problémy. Později získaná velká čísla mají větší rozptyl než časná měření a problémem se stává jejich srovnání běžnými statistickými metodami. Někdy ani nelze všechny hodnoty přehledně zachytit v jednom grafu. Transformace dat upravující numerický rozsah hodnot zde rovněž stabilizuje rozptyl měření a umožňuje grafické zpracování souboru.
- Jiným typickým příkladem může být studium vlivu stresového faktoru na biologický systém, např. bakteriální kulturu. Část populace je vůči aplikovanému faktoru rezistentní a nereaguje, u citlivých jedinců naopak dojde k snížení metabolické aktivity. Výsledné rozložení hodnot se změní ze symetrického na asymetrický tvar a nastane problém se srovnatelností souborů s různým tvarem rozložení.
- Jsme pod tlakem požadavku zpracovat data výpočtem aritmetického průměru a směrodatné odchylky, avšak naše měření jsou rozložena silně asymetricky a aritmetický průměr není reprezentativním ukazatelem středu. Transformace převádějící primární data na normální tvar rozložení umožní aplikovat požadovanou metodiku hodnocení, byť až na transformovaných hodnotách.
V následující části se pokusíme vysvětlit principy a přínos transformace dat na nejčastěji používané formě, tedy logaritmování dat.
Logaritmická transformace jako nejčastěji aplikovaná metoda
Logaritmickou transformací dat se míní převod primárních dat do logaritmického tvaru pomocí přirozeného nebo jiného typu logaritmu. Logaritmická transformace efektivně zasahuje především u asymetrických rozložení zešikmených doprava, tedy s odlehlými vyššími hodnotami (obr. 1). Toto rozložení se modelově nazývá logaritmicko-normální (někdy také log-normální). Logaritmování je doporučeno především pro soubory s velkým numerickým rozsahem takto rozložených hodnot, kdy nejvyšší číslo převyšuje nejmenší hodnotu 3x a více.
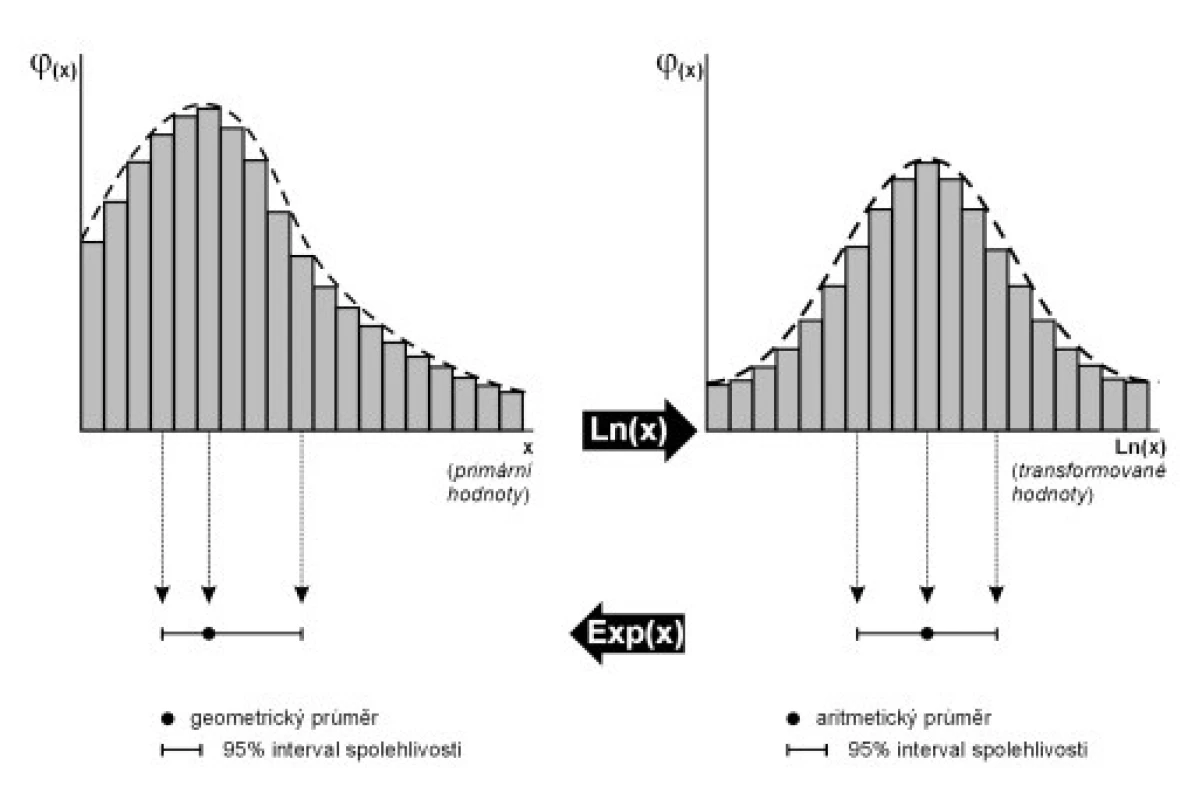

Logaritmická transformace nám pomáhá vyřešit v přírodě velmi častý typ asymetrie hodnot. Logaritmováním pozitivně zešikmeného rozložení dostaneme normální rozložení, u kterého již lze pracovat s běžným statistickým aparátem odhadu aritmetického průměru. Logaritmovat ovšem nelze naslepo, u jiných typů rozložení (obr. 1) nelze kýžený efekt očekávat. Logaritmování je nevhodné u dat, která již jsou v logaritmickém tvaru (např. pH hodnoty), a rovněž u nalevo zešikmených rozložení (tedy s nízkými odlehlými hodnotami).
Zpracované hodnoty lze následně publikovat přímo v logaritmickém tvaru, musíme to ovšem do tabulek i grafů jasně uvést (např. data in log scale, data logarithmically transformed, apod). U silně asymetrických nebo numericky proměnlivých parametrů toto doporučujeme především u grafů, které jsou v logaritmickém tvaru čitelnější a přehlednější. Mezi recenzenty vědeckých časopisů ale bývají zastoupeni puritáni vyžadující „čistou“ prezentaci primárních dat, a tam s logaritmovanými, ani jinak změněnými hodnotami neuspějeme. To ovšem nevadí, neboť po provedení potřebných výpočtů můžeme transformovaná data i výstupy výpočtů zpětně převést na původní jednotky exponenciální funkcí (obr. 1). Převádíme-li takto aritmetický průměr počítaný na logaritmovaných datech, získáváme v původních jednotkách tzv. geometrický průměr (geometric mean, GM). Tato statistika je pro nás v tomto seriálu nová, a proto jí věnujme určitý prostor. Zaslouží si to, neboť je v běžné klinické literatuře velmi nespravedlivě opomíjena.
Matematicky řečeno je geometrický průměr n-tá odmocnina součinu primárních hodnot. Výpočet se tedy podstatně liší od průměru aritmetického, místo sčítání zde hodnoty postupně násobíme. Nemáme-li k dispozici statistický program, lze vše pohodlně spočítat logaritmickou transformací hodnot dle postupu doloženého v tab. 1 nebo 2.
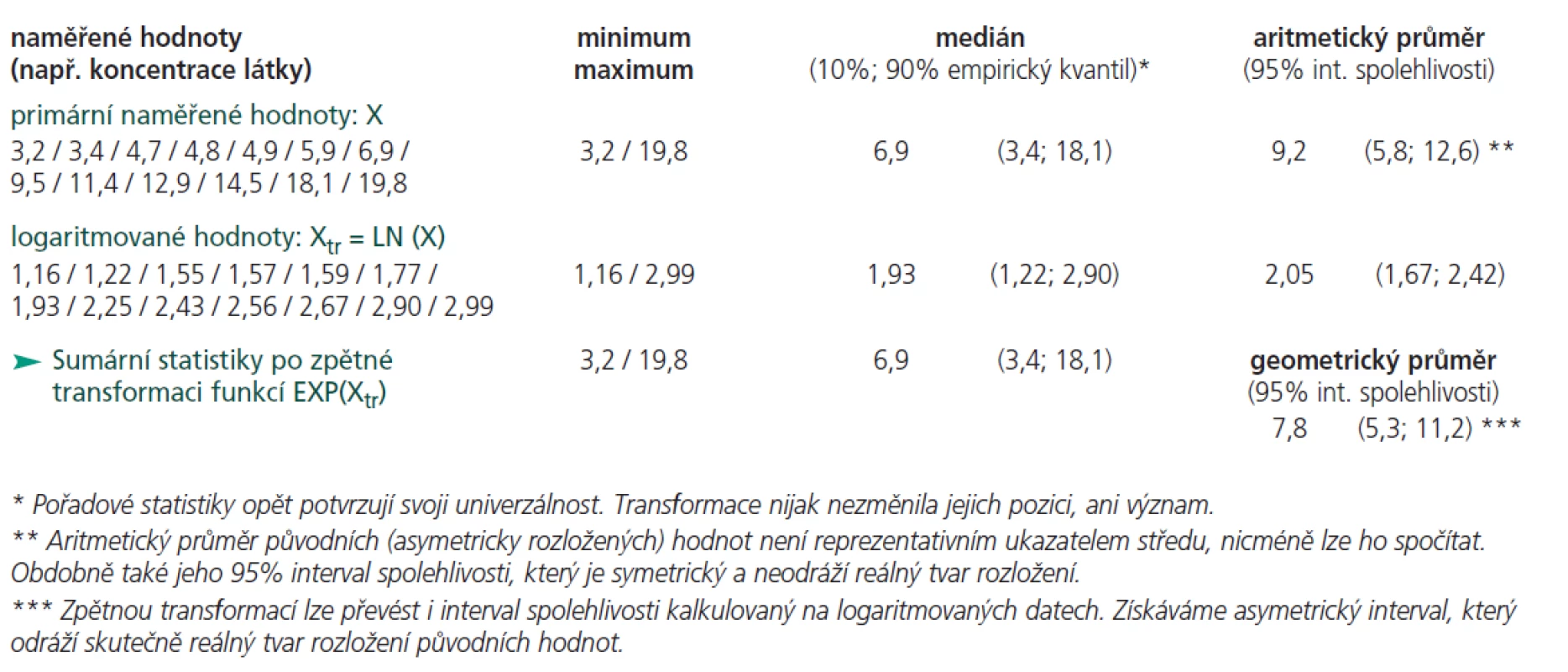
Geometrický průměr (GM) =
Nebo jinou formou zápisu: GM(x1, x2, x3) = (x1 . x2 . x3)1/3
U rozložení zešikmených doprava (obr. 1) leží geometrický průměr mezi mediánem a aritmetickým průměrem a výrazně lépe odráží reálný kvantitativní střed hodnot než aritmetický průměr. Je také méně citlivý na odlehlé hodnoty. Pro log-normální rozložení se tedy výpočet GM doporučuje nebo dokonce standardně předepisuje (např. v normách pro hodnocení kontaminace životního prostředí). Z klinických dat jsou vhodným kandidátem na výpočet GM například počty krevních buněk, neboť typicky vykazují log-normální tvar rozložení s častými odlehlými hodnotami.
* Pořadové statistiky opět potvrzují svoji univerzálnost. Transformace nijak nezměnila jejich pozici, ani význam.
** Aritmetický průměr původních (asymetricky rozložených) hodnot není reprezentativním ukazatelem středu, nicméně lze ho spočítat. Obdobně také jeho 95 % interval spolehlivosti, který je symetrický a neodráží reálný tvar rozložení.
*** Zpětnou transformací lze převést i interval spolehlivosti kalkulovaný na logaritmovaných datech. Získáváme asymetrický interval, který odráží skutečně reálný tvar rozložení původních hodnot.
Jakkoli je vzorec pro výpočet geometrického průměru poněkud nepěkný, lze z něj vyčíst ideální aplikaci této statistiky. Všimněte si, že jednotlivé hodnoty parametru X se mezi sebou násobí, a tak se vzájemně multiplikují. Proto je geometrický průměr užitečným ukazatelem středu u dat, která vyjadřují procentickou změnu hodnot (tzv. rate data). Už sama podstata takových dat totiž implikuje vzájemné násobení. Mějme 5 po sobě následujících měření vyjadřujících měsíční změnu hodnoty parametru X v % (mitotická aktivita buněk v tkáňové kultuře, kostní denzita, odezva nervových vláken, apod) – viz modelová data v tab. 3. Pokud bychom procentické změny sumarizovali např. mediánem nebo aritmetickým průměrem, dostali bychom velmi problematické výstupy. Geometrický průměr se zde ideálně hodí, neboť umožní sumarizovat relativní nárůst i pokles hodnot a výsledkem je interpretovatelná průměrná relativní změna daného parametru. Dalším typickým příkladem pro správnou aplikaci geometrického průměru by mohly být růstové nebo metabolické rychlosti, případně vývoj obratu nebo ekonomických nákladů v čase.

Je tedy evidentní, že geometrický průměr není samoúčelná míra, u asymetrických rozložení může vhodně nahradit aritmetický průměr a u poměrových indexů je statistikou s vysokou interpretační hodnotou. Výpočet GM ale není bez omezení. Jako statistika středu je definován pro soubory kladných reálných čísel, čímž se myslí nenulových čísel. Pokud se v souboru vyskytne nula, nemá výpočet GM smysl, neboť tato vynuluje součin hodnot. Tento problém se týká logaritmické funkce obecně, neboť nulu nejde logaritmovat. Zde nabízíme určitá řešení takové situace:
- Použití pozměněné transformace Xtr = Ln (X + 1).
- Nahrazení nulových hodnot jinými kvantitativními hodnotami. Například u laboratorních hodnot to může být polovina detekčního limitu. Nulové hodnoty lze také substitučně nahradit hodnotou 1, která následně nezmění součin ve vzorci pro GM a informace o daném vzorku zůstane zachována. Takové substituční postupy ale mají své kritiky a musí být jasně zdůvodněny.
Další typy statistické transformace dat a závěr
V podstatě jakoukoli matematickou funkci lze zapojit do transformace dat. Kromě logaritmování se v praxi relativně často uplatňují následující postupy:
- Odmocninová transformace je efektivní pro dosažení homogenity rozptylu u rozložení Poissonova typu, kde je rozptyl úměrný průměrné hodnotě. Na primární data je jednoduše aplikována druhá odmocnina. Při aplikaci je nutné kontrolovat vstupní data a výsledný efekt. Čísla mezi 0 a 1 se budou chovat jinak (zvětšovat hodnotu) než čísla > 1 (tato se budou snižovat). Druhá odmocnina ze 4 je 2, z 0,40 je to 0,63. Nedoporučuje se tedy takto ošetřovat proměnné s hodnotami < 1 a zároveň > 1 .
- Inverzní transformace jednoduše převádí primární data x do podoby 1/x. Tato funkce přirozeně dělá z malých čísel velká a naopak a bez předchozích úprav na primárních datech tedy převrátí pořadí hodnot. Funkce může sloužit jako normalizační pro hodnoty s exponenciálním rozložením.
- Arcsin transformace je doporučena pro soubory relativních hodnot, tedy podílů ležících numericky mezi 0 a 1. Velmi často je aplikována až na druhou odmocninu těchto čísel. Vhodná i pro normalizaci souborů s velmi malými podíly.
Takto bychom mohli pokračovat samozřejmě dále, nicméně vymezený prostor to neumožňuje. Schováme se tedy za velmi praktickou radu. Pokud tvar rozložení nebo hodnoty rozptylu vámi analyzovaných dat dělají problémy i po aplikaci jednoduchých transformačních funkcí, obraťte se raději s prosbou o konzultaci na odborníky – matematiky. U transformace dat se totiž musí postupovat citlivě, aby složitost samotné transformace nezastínila analyzovaný problém.
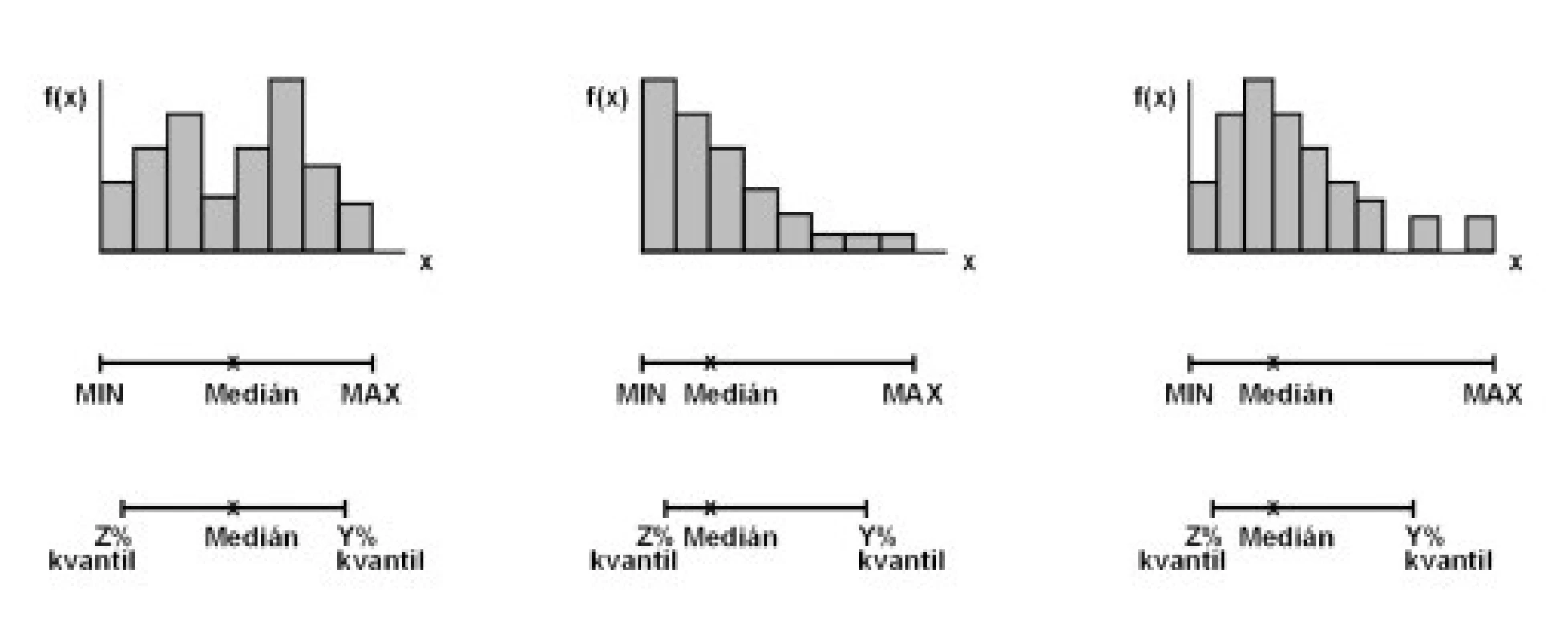
Snad se nám povedlo představit transformaci jako užitečnou formu úpravy primárních dat, nad kterou si analytik může udržet plnou kontrolu. Závěrem je ovšem nutné připomenout, že do transformace dat není třeba se nutit, pokud nás k tomu nevedou vážné důvody. Jak jsme již doložili v předchozích kapitolách, jakékoli typy rozložení umíme sumarizovat pomocí robustních pořadových statistik (medián, vybrané empirické percentily - kvantily). Jak je patrné z obr. 2, tyto statistiky umí reprezentativně podchytit i velmi asymetrická rozložení a nijak netrpí výskytem odlehlých hodnot. Kdykoli tedy selže pokus o transformaci dat, máme v záloze tuto přímočarou a velmi snadno interpretovatelnou formu prezentace.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz,
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Štítky
Dětská neurologie Neurochirurgie NeurologieČlánek vyšel v časopise
Česká a slovenská neurologie a neurochirurgie

2007 Číslo 5
Nejčtenější v tomto čísle
- Léčba epileptických syndromů u dětí
- Hodnocení edému terče zrakového nervu
- Jsou některé kontraindikace lumbální punkce dnes již obsoletní? Kazuistika
- Transforaminální lumbo-sakrální mezitělová fúze (TLIF) s instrumentací: prospektivní studie s minimálně 20měsíčním sledováním

