Analýza dat v neurologii LXVIII.
Úvod do korelační analýzy
Autoři:
L. Dušek; T. Pavlík; J. Jarkovský
; J. Koptíková
Působiště autorů:
LF MU, Brno
; Institut biostatistiky a analýz
Vyšlo v časopise:
Cesk Slov Neurol N 2018; 81(2): 235-237
Kategorie:
Okénko statistika
V tomto díle seriálu otevíráme zcela novou oblast statistických analýz, kterou zastřešuje název korelační analýza (corrrelation analysis). Již z názvu je patrné, že půjde o velmi často využívané metodiky, bez kterých si zpracování klinických dat nelze představit. Slovo korelace zdomácnělo i v běžné mluvě a obecně se jím rozumí vztah dvou znaků, charakteristik. Pokud hodnoty jednoho znaku rostou či klesají úměrně k hodnotám znaku druhého, hovoříme o pozitivní (kladné) korelaci; je-li vývoj hodnot obou znaků opačný, pak jde o korelaci negativní (zápornou). Hodnotíme tak např. pozitivní či negativní korelaci různých charakteristik pacienta nebo nemoci, korelaci mezi léčebnou odpovědí a dávkou léku, apod. Obsahem korelační analýzy je jednak spolehlivý odhad (kvantifikace) velikosti (síly) dané korelace, jednak posouzení její statistické významnosti. V dalších dílech seriálu budeme představovat různé ukazatele korelace, jejich interpretaci a testy hodnotící jejich statistickou významnost.
Velkou část našeho seriálu jsme již v minulosti věnovali rozboru vzájemné asociace binárních či kategoriálních proměnných, např. v analýze kontingenčních tabulek (díly 35– 45), kde kvantitativní mírou vztahu byl odhad poměru šancí (odds ratio) nebo relativního rizika (relative risk). Pojmem korelační analýza definičně označujeme rovněž kvantifikaci vzájemného vztahu proměnných, které jsou ale kvantitativní, poměrové (viz též díl 1 seriálu). Zkoumání vzájemné relace takových charakteristik se nemusí omezovat pouze na průkaz existence vztahu, ale umožňuje i odpovídat na otázky „o kolik nebo kolikrát narůstá nebo klesá hodnota proměnné Y při jednotkové změně hodnoty proměnné X“. Tato data totiž umožňují interpretovat i podíl hodnot vyjadřujících intenzitu dané vlastnosti, přičemž nulová hodnota často není slučitelná s existencí subjektu, a vztah tak začínáme zkoumat až od určité číselné hranice (např. hmotnost pacienta, krevní tlak apod.).
S výše uvedeným úzce souvisí i rozšiřující se grafické možnosti pro znázornění zkoumaného vztahu, neboť kvantitativní charakteristiky lze proti sobě vykreslit do bodového grafu (scatter plot). Jde o diagram, v němž je každá dvojice pozorování (Xi– Yi) znázorněna jako bod v pravoúhlé souřadnicové soustavě. Body grafu tvoří množinu, z níž lze zkoumaný vztah snadno posoudit vizuálně.
Příklad 1 graficky znázorňuje vybrané modelové situace takových vztahů. Grafy 1A, B ukazují silný lineární vztah dvou proměnných, kdy jednotlivé body leží téměř na přímce. Takové vztahy pozorujeme typicky při kalibračních laboratorních měřeních, v reálné klinické praxi bývají body kolem pomyslné přímky více rozptýleny, jak ukazují grafy 1 D, E. Rostoucí rozptyl hodnot existenci vztahu maskuje až do bodu, kdy mezi oběma proměnnými není pozorovatelný žádný vztah a následná analýza by rozptýlení bodů označila jako náhodné (graf 1F).

Z hlediska statistického hodnocení tak posuzujeme pravděpodobnost výskytu hodnot proměnné Y v relaci k hodnotám, kterých nabývá proměnná X. U nejsilnějších vztahů (absolutní, maximální korelace) náleží každé hodnotě X právě jedna hodnota Y a body v X– Y grafu by přesně ležely na přímce. A naopak, při neexistenci korelace je výskyt všech možných hodnot Y stejně pravděpodobný pro všechny hodnoty X.
V učebnicích se často zjednodušeně uvádí, že cílem korelační analýzy je určit sílu lineární závislosti mezi veličinami. My se pokusíme v dalších dílech seriálu čtenáře přesvědčit, že záběr této oblasti statistiky je širší a rozhodně se neomezuje pouze na lineární vztahy, tedy na vztahy, které lze vyjádřit přímkou. Vztah mezi kvantitativními proměnnými ovšem nemusí být zdaleka vždy lineární. Graf 1C v příkladu 1 zobrazuje parabolu, kde od určité hodnoty proměnné X hodnota Y již dále nenarůstá a naopak začíná klesat. Nelineární závislosti jsou typické pro experimenty „dávka – účinek“, kde rostoucí dávka zkoumané látky má nejprve stimulující účinek na biologický systém, avšak od určité hranice se tento efekt nasytí a účinek již dále neroste, nebo mají vyšší dávky dokonce efekt opačný, tedy toxický. Matematický popis a kvantifikace nelineárních vztahů jsou samozřejmě složitější než v případě přímky. Touto problematikou se budeme zabývat až po výkladu analýzy vztahů lineárních. Avšak již zde můžeme zobecnit, že v přírodě i v reálné klinické praxi pozorujeme častěji nelineární vztahy proměnných než vztahy přímkové. Již samo zobrazení a určení typu takového vztahu bývají velmi významné, neboť různé nelineární vztahy mají různé a často velmi zásadní interpretace. Proto je důležité analýzu vztahů kvantitativních proměnných neomezovat pouze na učebnicový příklad přímky.
V případě, kdy mezi veličinami X a Y existuje definiční vztah (např. vztah hmotnosti tělesa a jeho objemu), hovoříme o funkční závislosti. Takový vztah se graficky projeví jasně zřetelným typem závislosti, např. přímkou, téměř bez rozptýlení bodů kolem ní. Těmto vztahům se rovněž říká deterministické. Je-li proměnná Y v přímém lineárním vztahu k proměnné X, můžeme tento fakt vyjádřit rovnicí:
Y = k × X
nebo obecněji Y je funkcí X
Y = f(X).
Při zkoumání charakteristik reálných biologických systémů nacházíme takto definičně dané závislosti jen zcela výjimečně. Mnohem častěji je třeba popsat závislosti, kdy mezi sledovanými znaky (náhodnými proměnnými) neexistuje deterministický vztah, resp. je tento vztah částečně maskován rozptylem hodnot sledovaných proměnných a experimentátorovi není předem znám. Učebnicovým příkladem může být vztah mezi hmotností lidí a výškou jejich postavy. Principiálně zde očekáváme silnou a pozitivní korelaci, avšak nikoli funkční lineární závislost. V těchto případech hovoříme o statistické (stochastické) závislosti proměnných a právě na ni je zaměřena statistická korelační analýza. Statistická významnost korelace zde určuje existenci vztahu průkaznou nad variabilitou hodnot obou korelovaných proměnných.
Z grafů v příkladu 1 vyplývá velmi podstatná podmínka korelační analýzy, kterou si zde dovolíme zdůraznit, ačkoli ji čtenáři zřejmě budou považovat za samozřejmost. Každý bod v grafech příkladu 1 představuje jeden konkrétní subjekt (např. pacienta), na kterém byly zároveň naměřeny hodnoty X i Y. Korelační analýza tak vychází z dat párově uspořádaných experimentů, kde jsou hodnoty X a Y měřeny na témže subjektu, a má tedy a priori smysl ptát se na jejich vzájemný vztah. Pokud by tomu tak nebylo, nebude mít korelační analýza ani grafické znázornění hodnot smysluplnou interpretaci. Přesto se i v odborné literatuře korelace vyhodnocuje v situacích, kdy věcně nemůže mít přínosnou interpretaci. Tzv. nesmyslným korelacím budeme věnovat jeden z příštích dílů seriálu.
Modelový datový záznam vstupující do korelační analýzy schematicky prezentuje tab. 1:
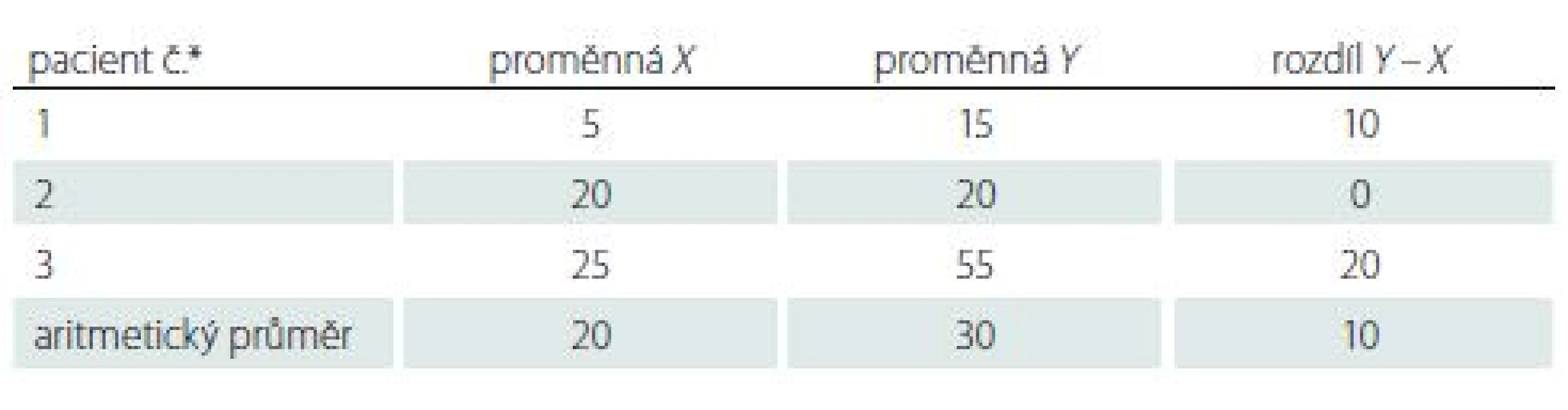
Zvláštní interpretaci mají korelační analýzy, které mají prediktivní význam. Vraťme se opět ke grafům v příkladu 1. Proměnná X by zde mohla znamenat charakteristiku jedince v dětském věku a proměnná Y stejnou nebo jinou charakteristiku v dospělosti. Například zda výška v určitém věku dítěte predikuje výšku v dospělosti či zda obezita v dětském věku predikuje tyto problémy i následně během života.
Další velmi významná poznámka se rovněž týká obecné interpretace korelací zjištěných vztahů. Statistický průkaz závislosti proměnných demonstrovaných např. na grafech 1A, B v příkladu 1 automaticky neznamená, že daný vztah má interpretační vysvětlení a vyplývá z něj příčinná souvislost mezi proměnnými. Interpretace vztahu vždy vyžaduje další analýzy a zejména průkaz příčinné souvislosti se musí opírat o podstatně širší důkazovou základnu než jen o statisticky významnou korelaci (viz též díl 59 seriálu). Mnozí autoři studií na tento fakt zapomínají, a proto se také o korelaci hovoří jako o jedné z nejčastěji zneužívaných statistik.
Pojem korelace tedy znamená existenci vzájemného vztahu mezi veličinami X a Y, avšak v žádném případě neimplikuje kauzalitu vztahu. Při korelaci se při změně jedné veličiny mění korelativně i veličina druhá. Je tudíž pravděpodobné, že na sobě závisejí. Nelze z toho však usuzovat, že jedna veličina je příčinou a druhá následkem. Z tohoto důvodu nejsou osy bodových grafů v příkladu 1 nijak prioritně dány, z hlediska korelace tedy můžeme proměnné na vodorovné a svislé ose bodových diagramů libovolně zaměnit. Rovněž je důležité zdůraznit, že ani nulová korelace nevylučuje vztah mezi sledovanými proměnnými. Této problematice se budeme věnovat podrobněji v dalším díle seriálu, ve kterém vysvětlíme klíčové pojmy kovariance a korelační koeficient.
doc. RNDr. Ladislav Dušek, Ph.D.
Institut biostatistiky a analýz, LF MU, Brno
e‑mail: dusek@iba.muni.cz
Štítky
Dětská neurologie Neurochirurgie NeurologieČlánek vyšel v časopise
Česká a slovenská neurologie a neurochirurgie

2018 Číslo 2
Nejčtenější v tomto čísle
- Ataxie
- Biopsie mozku v deseti bodech – co může neurolog očekávat od neurochirurga a neuropatologa?
- Fabryho choroba, přehled problematiky a nejčastější neurologické projevy
- Prof. MUDr. Pavel Haninec, CSc. slaví 60 let
