Analýza dat v neurologii
XXV. Hodnocení diagnostických testů – senzitivita a specificita
Autoři:
L. Dušek; T. Pavlík; Jiří Jarkovský
; J. Koptíková
Působiště autorů:
Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise:
Cesk Slov Neurol N 2011; 74/107(1): 97-103
Kategorie:
Okénko statistika
V dílech XX–XXIV seriálu jsme se věnovali kategoriálním znakům a kontingenčním tabulkám. Toto téma ještě neopustíme a budeme ho rozvíjet především s důrazem na klinické aplikace. Proto jsme zde zařadili analýzu výstupů diagnostických testů jako jeden z klasických příkladů hodnocení tabulek četností. Nejprve se budeme věnovat diagnostickým testům, jejichž výstupem jsou kategoriální data (tedy výstupy ve formě ano/ne; pozitivní//negativní), v dalších kapitolách seriálu se zaměříme na testy produkující spojité, kvantitativní hodnoty. Jak dále uvidíte, nejde jen o pouhé opakování statistických analýz. Tato oblast pracuje se specifickými pojmy a měřítky kvality testů, které již zdomácněly i v klinické praxi.
V úvodu musíme zdůraznit, že pod pojmem „diagnostické testy“ zde nemyslíme jen laboratorní postupy vedoucí k analýzám odebraných vzorků tkání. Stejný typ výsledků vyžadující stejné hodnocení nabízí jakýkoli metodicky jasně popsaný diagnostický postup směřující k poznání, zda pacient má nebo nemá nějaký typ problému či nemoci. Níže uvedenými postupy tedy můžeme hodnotit i výstupy psychologických testů, psychiatrických vyšetření nebo sumarizovat sledování kvality života pacientů.
Statistické hodnocení diagnostických testů se týká především experimentů, kdy je konkrétní test verifikován pro další závazné použití v praxi. Výstupem analýz jsou potom ukazatele celkové správnosti výsledku testu a jeho tzv. diagnostické prediktivní hodnoty. Běžně také hodnotíme míru chybovosti testu, ze které usuzujeme na rizika spojená s jeho použitím (nerozpoznání nemoci u pacienta, chybné označení nemoci u zdravého člověka). Tento typ analýz vyžaduje srovnání výsledků testu (pozitivní/negativní) proti skutečně verifikovanému stavu nemocného (nemoc prokazatelně přítomna/nepřítomna). Ve fázi validace tedy musíme mít soubor dat, kde daný test zkoušíme na souboru jedinců, jejichž zdravotní stav je již prokázán jinými, objektivními metodami (referenční testy nebo jiná forma verifikace diagnózy). Pokud daný test v tomto srovnání obstojí, lze jej zařadit do sady klinicky využitelných postupů. Srovnání výsledků testu s verifikovanou skutečností je jediným relevantním validačním postupem.
Druhým typem hodnocení výsledků diagnostických metod je přímé srovnání výstupů dvou testů na souboru n jedinců nebo vzorků. Může jít o srovnání dvou laboratorních postupů, přístrojů nebo i zcela rozdílných metod určení diagnózy. Zde většinou nemáme ambici závazně verifikovat výsledek jedné z metod proti metodě druhé, spíše jde o zjištění jejich vzájemné shody a nahraditelnosti. Z hlediska statistiky testujeme nulovou hypotézu, že se obě srovnávané metody ve výsledku neliší. Nutně jde o párové uspořádání experimentu, neboť obě metody musí být testovány na stejné sadě vzorků nebo jedinců. Pro takové experimenty jsme již správné postupy hodnocení uvedli v díle XXIII seriálu; vhodný je především McNemarův test. Pro odhad rozdílu ve výsledcích srovnávaných metod je někdy požadován výpočet intervalu spolehlivosti, který pro tento typ experimentu uvádíme v příkladu 1.

Jednoduše řečeno, od diagnostických testů požadujeme, aby byly správné a přesné. Oba tyto pojmy se vztahují ke kvalitě diagnostiky a někdy bývají nesprávně zaměňovány. Správností výsledku testu se budeme zabývat v dalším textu této kapitoly, kde budeme z hlediska diagnostiky nemoci rozlišovat správnost určení diagnózy (pozitivní nález), správnost zamítnutí diagnózy (negativní nález) a správnost celkovou, která obě uvedené možnosti spojuje. Správnost testu definujeme jako jeho schopnost maximálně se přiblížit skutečné hodnotě. Naopak přesnost je vlastnost testu vyjadřující shodu (maximální přiblížení) výsledků z opakovaných měření. Rozlišujeme přitom opakovatelnost výsledku (měříme na stejné sérii vzorků) a reprodukovatelnost výsledku, kdy měření provádíme mezi různými sériemi vzorků nebo je provádějí různí pozorovatelé či analytici. Statistickým hodnocením přesnosti a reprodukovatelnosti jsme se již zabývali v dílech VI–VII našeho seriálu. Rozdíl mezi správností a přesností výsledků testu schematicky znázorňuje obr. 1.
![Správnost a přesnost výsledků diagnostických testů ve schematickém znázornění, upraveno dle [1].](https://www.csnn.eu/media/cache/resolve/media_object_image_small/media/image/adc0e07a00faa963c4c6e69b9961435b.jpeg)
Vraťme se ale k učebnicovému příkladu, kdy výsledek testu stojí proti známé skutečnosti, a my hodnotíme, do jaké míry se test s realitou shoduje. Pro potřeby praxe využíváme sadu ukazatelů, které přinášejí hodnotnou interpretaci výsledku především ve vztahu k chybovosti zkoumaného testu. Nejčastěji používanými pojmy jsou senzitivita, specificita, celková přesnost, prediktivní hodnota pozitivního a negativního výsledku testu. Jejich definici a zjednodušený výpočet uvádí tab. 1.
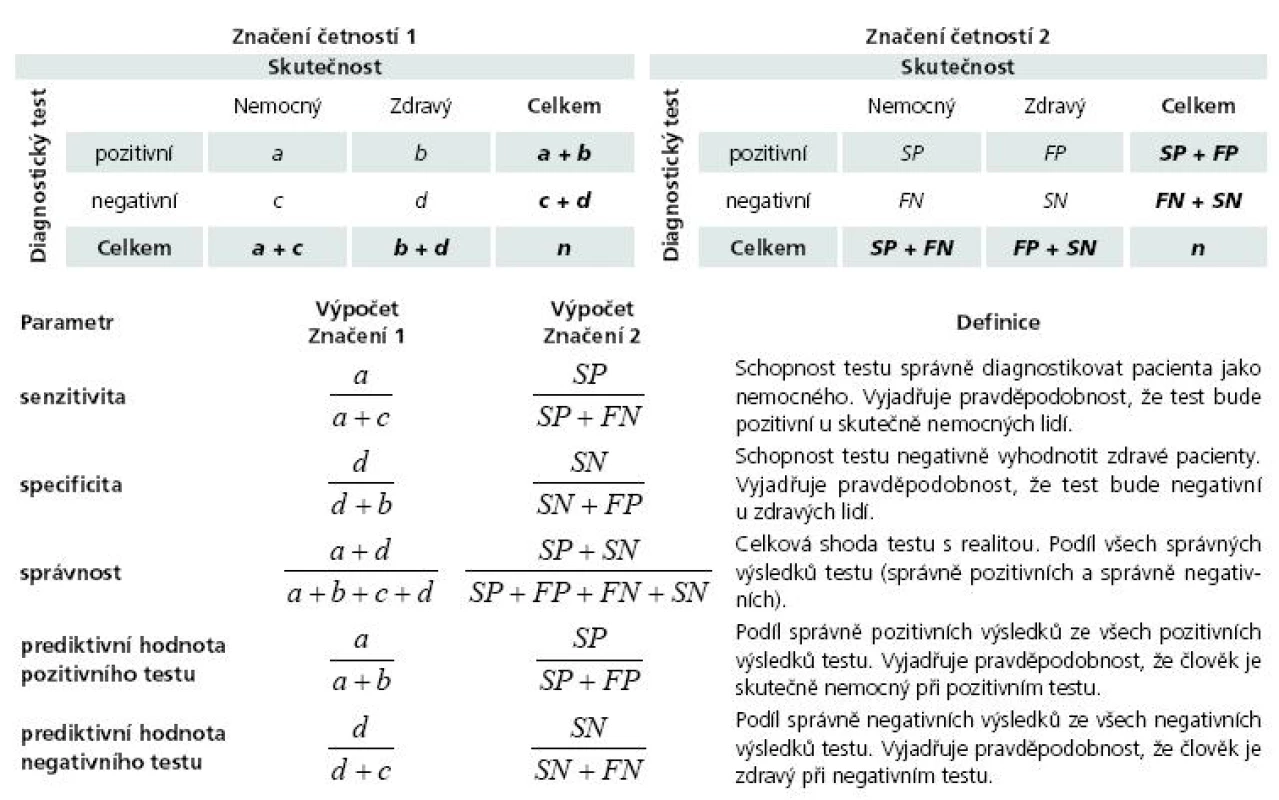
Doufáme, že výpočty v tab. 1 jsou přehledné, ačkoli v nich uvádíme dva alternativní způsoby značení výpočtu. Činíme tak s přesvědčením, že zvláště značení využívající pojmy FN a FP (falešně negativní a falešně pozitivní výsledek) přispěje k vysvětlení významu jednotlivých ukazatelů.
Z tab. 1 vyplývá, že senzitivita není jen prostý podíl pozitivně diagnostikovaných jedinců, jak někdy bývá zjednodušeně a nesprávně interpretována. Jde o komplexní ukazatel, který vyjadřuje schopnost testu být pozitivní u nemocných jedinců. Hodnota senzitivity je tedy ve jmenovateli snižována počtem falešně negativních výsledků, neboť tito jedinci měli být správně diagnostikováni jako pozitivní, ale test je tak nezařadil. Obdobně specificita vyjadřuje schopnost testu být negativní u zdravých jedinců, a její hodnotu tak ve výpočtu snižují počty falešně pozitivních osob, tedy zdravých jedinců nesprávně označených za nemocné. Není tedy pravda, že roste-li počet pozitivních výsledků testu, musí automaticky narůstat jeho senzitivita. Tento trend neplatí zejména tehdy, je-li velký podíl výsledků pozitivních falešně anebo je v daném experimentu velký podíl falešných negativit (tedy ve skutečnosti nemocných jedinců, které ale test neurčil jako pozitivní). Z tohoto důvodu má velký smysl oba ukazatele doplnit výpočtem celkové správnosti, který čtenáři usnadní interpretaci výsledku (tab. 1).
Senzitivita a specificita nevypovídají o diagnostické hodnotě testu zcela vyčerpávajícím způsobem, neboť hodnotí výsledky jen z pohledu srovnání „výsledek vs skutečnost“. Avšak v klinické praxi je výsledek testu jedinou informací, kterou má diagnostikující lékař k dispozici. Diagnostickou prediktivní hodnotu testu tedy určuje, do jaké míry (s jakou pravděpodobností) platí, že jedinec s negativním testem je skutečně zdráv, a naopak s jakou pravděpodobností je jedinec s pozitivním testem skutečně nemocen. V prvním případě hodnotíme podíl správně určené negativity ze všech negativních výsledků testu, ve druhém pak podíl správně pozitivních výsledků mezi všemi pozitivními výsledky (tab. 1). Je zřejmé, že výpočet těchto ukazatelů závisí na rozdělení četností ve výsledkové tabulce a samozřejmě také na velikosti vzorku n. Ačkoli jsou výpočty uváděné v tab. 1 zdánlivě obdobné, vedou k parametrům se zcela odlišnou interpretací a významem.
Často slýcháme otázku, jaké hodnoty senzitivity a specificity jsou již dostatečné, průkazné nebo významné. Odpověď bohužel není jednoduchá, neboť do značné míry závisí na stavu poznání dané oblasti a na dosažitelné správnosti dostupných testů. V určité oblasti mohou být hodnoty nad 60 % vítězstvím, v jiné se diagnostika blíží v obou ukazatelích hodnotě 100 % (tedy téměř se nevyskytují falešně pozitivní a falešně negativní nálezy). V každé oblasti existují objektivní limity dané úrovní diagnostiky. Nicméně relevanci odhadu specificity a senzitivity určuje také kvalita experimentu, a to především ve dvou aspektech:
dostatečná velikost vzorku zvyšuje kvalitu a přesnost provedených odhadů; při malém n roste pravděpodobnost, že některé typy výsledků nezachytíme a odhady specificity a senzitivity budou zkreslené
reprezentativnost vzorku určující rozdělení četností v tabulce; je-li například podíl nemocných a zdravých jedinců v populaci 1 : 4, měl by být takto ideálně zachován i ve sbíraném vzorku – získáváme tím realistický základ pro posouzení skutečné prediktivní hodnoty testu.
Velmi dobře dosažitelným a přitom v odborných článcích málo využívaným způsobem, jak vyjádřit kvalitu odhadu senzitivity a specificity, je výpočet jejich intervalu spolehlivosti. Z rozsahu jeho hodnot lze rychle posoudit, jakou relevanci mají vlastní bodové odhady. Senzitivita a specificita jsou v podstatě podíly (relativní četnosti), a tudíž pro výpočet intervalu spolehlivosti můžeme za určitých předpokladů využít model pro binomické rozdělení pravděpodobnosti. Výpočet dokumentovaný v příkladech 2–3 není složitý a lze jej lehce provést i bez specializovaného softwaru.


Pozorného čtenáře dále jistě napadlo, zda by se při hodnocení diagnostického testu nedal využít nějaký statistický test posuzující významnost shody výsledků diagnostiky a skutečnosti. Jelikož výsledkem je v našem příkladu vždy tabulka četností 2 × 2, lze ji obecně hodnotit již dříve vysvětlenými χ2 testy. Statistická významnost testu by zde prokazovala významnou, a tedy nenáhodnou souvislost mezi výstupem testu a skutečností. Při hodnocení diagnostických testů je ale takové testování příliš obecné a interpretačně nenahradí výše popsané ukazatele. Od této běžné statistiky χ2 je dále odvozován tzv. koeficient phi, který nabývá hodnot od –1 do +1 (viz též díl XXI). Hodnota koeficientu +1 značí maximální pozitivní shodu výskytu sledovaných kategorií, hodnota –1 pak maximální negativní shodu a hodnota 0 znamená náhodné rozdělení četností v tabulce. Díky jasné interpretaci bývá tento koeficient doporučován jako ideální ukazatel míry vztahu (shody) dvou binárních znaků, a je tedy použitelný i pro případ srovnání diagnostického testu se skutečností. Koeficient phi bývá také někdy ve specializovaných softwarech označován jako Matthews correlation coefficient. Ukázky statistického hodnocení při validaci diagnostických testů jsou uvedeny v příkladu 4.

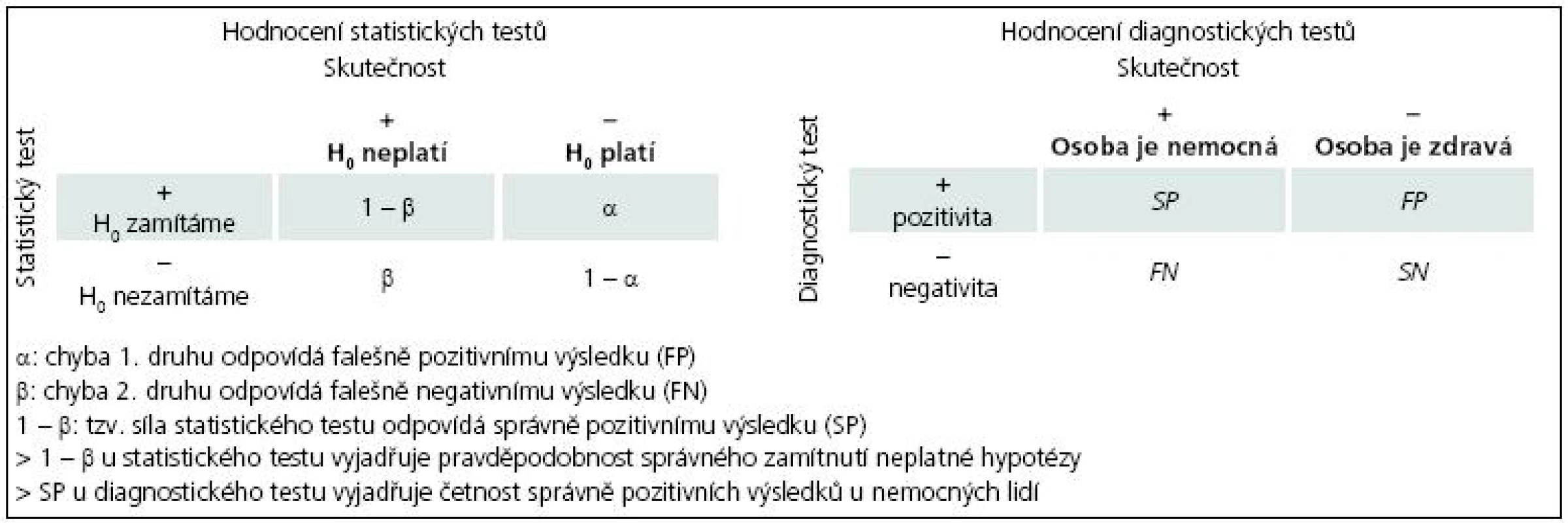
Na závěr si dovolíme připomenout, že zde probírané téma vlastně až tak nové pro čtenáře našeho seriálu není. Koncept hodnocení senzitivity a specificity je v podstatě totožný s pravděpodobnostní metodikou hodnocení statistických testů. Shodu obou konceptů přibližuje obr. 2.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Štítky
Dětská neurologie Neurochirurgie NeurologieČlánek vyšel v časopise
Česká a slovenská neurologie a neurochirurgie
2011 Číslo 1
Nejčtenější v tomto čísle
- Monitoring pacientů s těžkým poraněním mozku
- Lacosamid (Vimpat®) – nový lék pro přídatnou léčbu pacientů s fokální epilepsií
- Účinnost piracetamu, vinpocetinu a Ginkgo biloba na poruchy učení a paměti vyvolané antipsychotiky.
- Nadužívání léků pacienty s chronickou denní bolestí hlavy v České republice
