Analýza dat v neurologii. VII.
Reprodukovatelnost a opakovatelnost měření u spojitých dat
Autoři:
L. Dušek; T. Pavlík; J. Koptíková
Působiště autorů:
Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise:
Cesk Slov Neurol N 2008; 71/104(1): 106-109
Kategorie:
Okénko statistika
V minulém díle seriálu jsme se věnovali hodnocení reprodukovatelnosti a opakovatelnosti u diskrétních dat. Ovšem i u spojitých dat je toto hodnocení vyžadováno jako doklad kvality a serióznosti experimentální práce. A obdobně jako u dat diskrétních se zde v zahraniční literatuře operuje s pojmy inter-observer a intra-observer variabilita. Význam těchto pojmů se přechodem na spojitá data nijak nemění, zásadně se ale mění možnosti hodnocení.
U diskrétních dat nabývajících pouze omezeného počtu hodnot je analýza reprodukovatelnosti i opakovatelnosti založena na sledování frekvence shody v měření (viz též díl VI seriálu). Ve srovnání s tím nabízejí spojitá data širší možnosti, včetně instruktivních grafických znázornění. Logicky jsou tyto testy povinnou komponentou hodnocení kvality u diagnostických zkoušek a obecně u laboratorních měření.
Reprodukovatelnost je stejně jako u diskrétních dat nadřazeným pojmem, neboť sleduje výsledky opakovaných měření prováděných různými experimentátory. Předpokládáme tedy, že reprodukovatelné výsledky umožňují zavádění postupů v různých laboratořích, protože reprodukovatelnost výstupů mohou kontrolovat nezávislé osoby a instituce. Opakovatelnost vyjadřuje shodu opakovaného měření určité sady vzorků „v sérii“ od stejného experimentátora. K měření reprodukovatelnosti i opakovatelnosti je možné použít totožné vzorky. Nejjednodušší možný příklad, kdy je měření provedeno pouze 2x uvádí tab. 1.
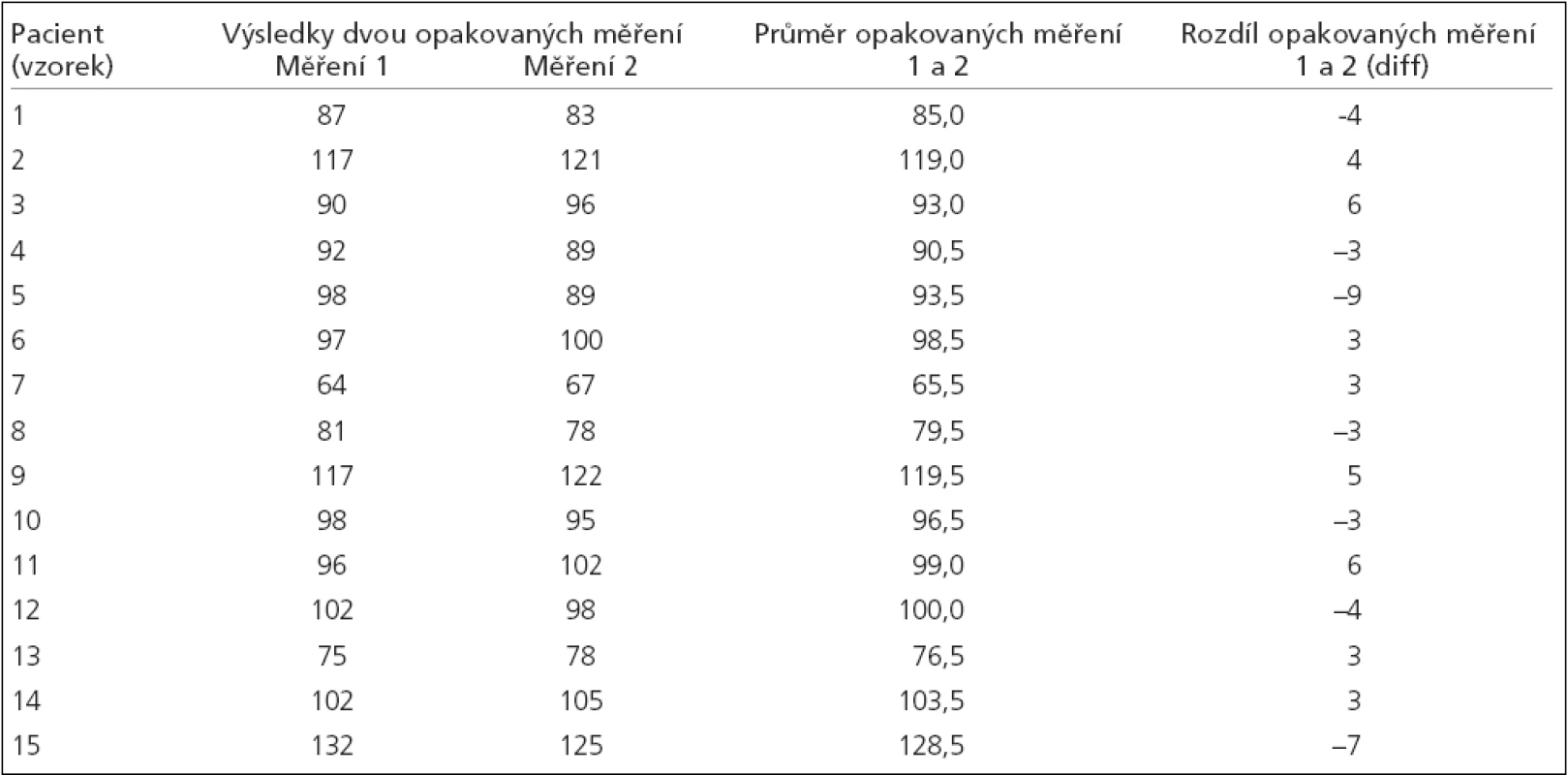
Měření 1 a 2 zde představují opakování experimentu nebo měření sady 15 vzorků. Podle toho, zda měření provedla jedna osoba nebo dva různí experimentátoři budeme hovořit o opakovatelnosti nebo reprodukovatelnosti výsledků. Obojí by nastalo ze 100 %, pokud by všech 15 párů měření poskytlo přesně stejný výsledek, což u hodnocení běžných biologických nebo chemických znaků v praxi nemůže nastat. Musíme tedy prověřit, o kolik se opakovaná měření liší (označeno jako sloupec diff) a vyhodnotit míru shody anebo neshody.
Hodnocení reprodukovatelnosti a opakovatelnosti je tedy kvantitativní analýzou odchylky opakovaných měření téhož znaku. Nejprve počítáme diference opakovaných měření (diff) a následně odhadujeme jejich průměr (̄xdiff) a směrodatnou odchylku (sdiff). Hodnota sdiff bývá označována jako směrodatná odchylka opakovatelnosti nebo reprodukovatelnosti. Další postup lze shrnout v následujících bodech:
- Vyhodnotíme, zda se průměr diferencí neliší od nuly. V ideálním případě je x̄diff přesně rovno nule (viz příklad v tab. 1) nebo se od nuly odchyluje jen nepodstatně. Významná odchylka průměru diferencí od nuly indikuje systematickou chybu („bias“), kdy jedno z opakovaných měření vede systematicky k vyšším nebo nižším hodnotám něž měření druhé. Odchylku průměru diferencí od nuly lze prověřit statistickým testem (např. t-test) nebo pro ni lze spočítat interval spolehlivosti.
- Vypočítáme tzv. limity shody opakovaných měření (limits of agreement). Za předpokladu, že diference opakovaných měření mají normální rozložení, můžeme limity pro výskyt 95 % diferencí počítat jako x̄diff ± 1,96*sdiff (místo 1,96 se používá i zaokrouhlená hodnota 2). Příklad v tabulce 1 vede k dolní hranici intervalu -9,6 a symetricky k horní hranici +9,6. Pokud jsou tyto limity v praxi akceptovatelné jako hranice přijatelného rozdílu opakovaných měření, pak je lze využít jako míru reprodukovatelnosti nebo opakovatelnosti. Pokud diference opakovaných měření dané hranice překračují, nelze měření označit za reprodukovatelná (opakovatelná).
- Použijeme grafické znázornění dle práce Bland a Altman (1986). Tento dnes již standardní graf (nazývaný téměř familiárně Bland&Altman plot) je znázorněn na obrázku 1a. Jednoduše vynášíme průměr opakovaných měření na osu X a jejich diference na osu Y. K ose Y jsou dále zakresleny pozice průměrné diference (v našich datech přesně 0) a pozice 95% limitů shody (viz výše výpočet v bodě 2).
Závěr hodnocení modelového příkladu z tabulky 1 je, že opakovaná měření 1 a 2 se podstatně neliší a splňují podmínku výskytu 95 % diferencí v intervalu ± dvě směrodatné odchylky (Bland a Altman, 1986). Průměrná diference je nulová a nepředpokládáme tedy žádné systematické zkreslení u opakovaně měřených hodnot.
Výše uvedené nastavení 95% limitů shody je funkční pouze při splnění předpokladu normality rozložení diferencí opakovaných měření. Tento předpoklad je nutné prověřit testy i graficky (např. histogram), k jeho posouzení významně přispěje i graf dle práce Bland a Altman (1986). Graf znázorněný na obrázku 1a umožní nejen posoudit shodu opakovaných měření, ale snadno identifikuje odlehlé body i jiné odchylky od normality (viz níže diskuze k obrázkům 3-4).
Limity shody x̄diff ± 1,96*sdiff se vztahují k výskytu všech diferencí v populaci a nelze je považovat za interval spolehlivosti odhadu x̄diff . Ten můžeme odhadnout dle standardního vzorce, s využitím standardní chyby odhadu průměru počítané jako sdiff /√n. Místo standardizovaného normálního rozložení zde musíme použít kvantil Studentova rozložení t pro n-1 = 14 stupňů volnosti. U dat z tabulky 1 je standardní chyba průměru diferencí 1,3 a kvantil t0,975 = 2,1. Můžeme tedy kalkulovat 95% interval spolehlivosti pro x̄diff s hranicemi ± 2,7. Obecně je interval spolehlivosti výpočet užitečný jako hodnocení systematického zkreslení opakovaných měření (bias). Jelikož je ale v našich datech průměr diferencí roven přesně nule, výpočet nemohl žádnou odchylku od nuly prokázat. Obdobně lze vypočítat i intervaly spolehlivosti pro spodní a horní limit shody. Zájemce o tento výpočet odkážeme na práce Bland a Altman (1986, 1999).
Pro praktickou práci s limity shody je nutné uvést ještě následující poznámky:
- Mezinárodně se používá alternativní termín „CR = coefficient of repeatability“. Jde jen o jiný název pro již uvedené 95% limity shody: CR = 1,96*[Σdiff2/(n-1)]1/2 = 1,96*sdiff. CR je tedy hranice, kterou za podmínek opakovatelnosti nebo reprodukovatelnosti nesmí absolutní hodnota diference opakovaných měření překročit.
- Limity shody se samozřejmě v praxi nepoužívají dogmaticky a z hodnocení je možné vyloučit ojedinělé zřetelně odlehlé body. Odlehlé body snadno identifikujeme na grafu, který modelově ukazuje obr. 1a.
- V praxi může nastat situace, kdy doporučené 95% limity shody nevyhovují, a to i přesto, že jde o dlouhodobě uznávaný standard (např. BSI, 1975). Je-li změna řádně zdůvodněna, lze využít jiné pravděpodobnostní hranice (90%, 99% apod.) anebo statistické hodnocení doplnit empirickým intervalem, který vychází ze znalosti dané metody měření, norem apod.
- Metodiku hodnocení reprodukovatelnosti lze také využít pro hodnocení shody různých metod, pokud měří stejnou veličinu. Příkladem může být posouzení nově zaváděné metody ve srovnání se starým postupem.
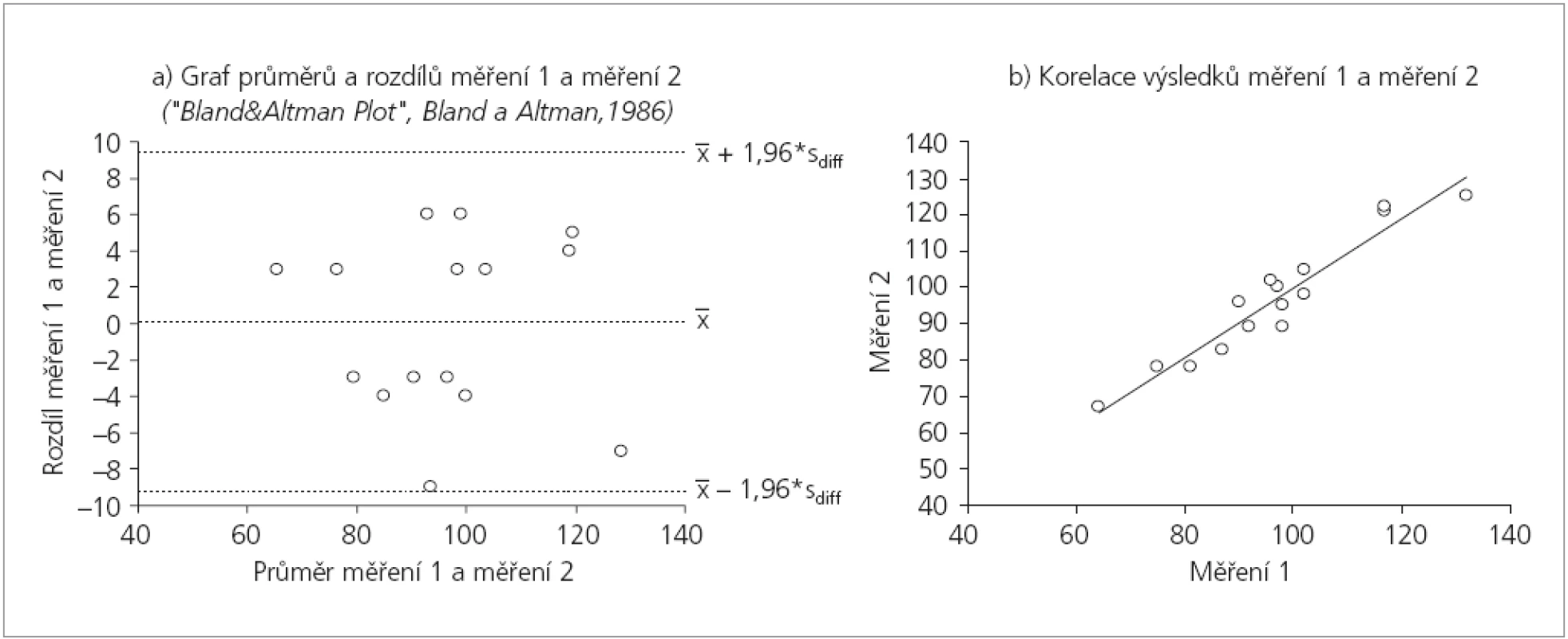
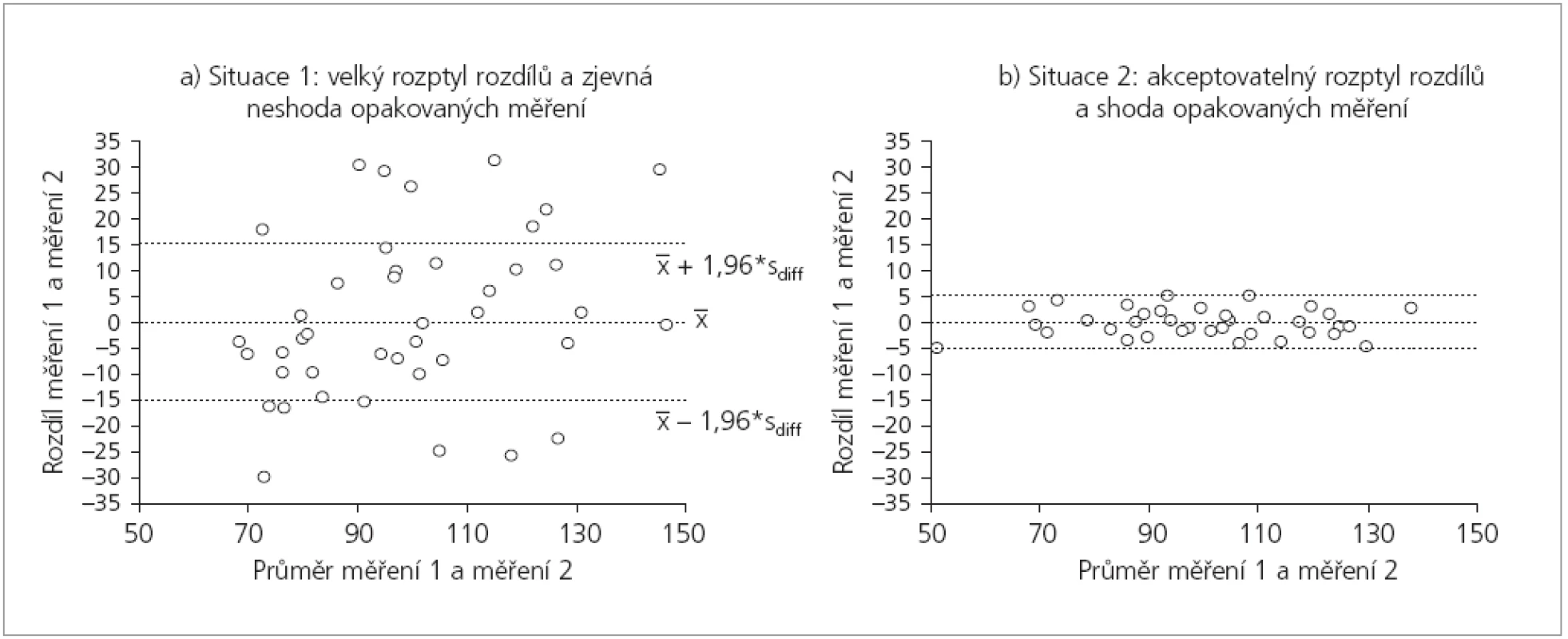
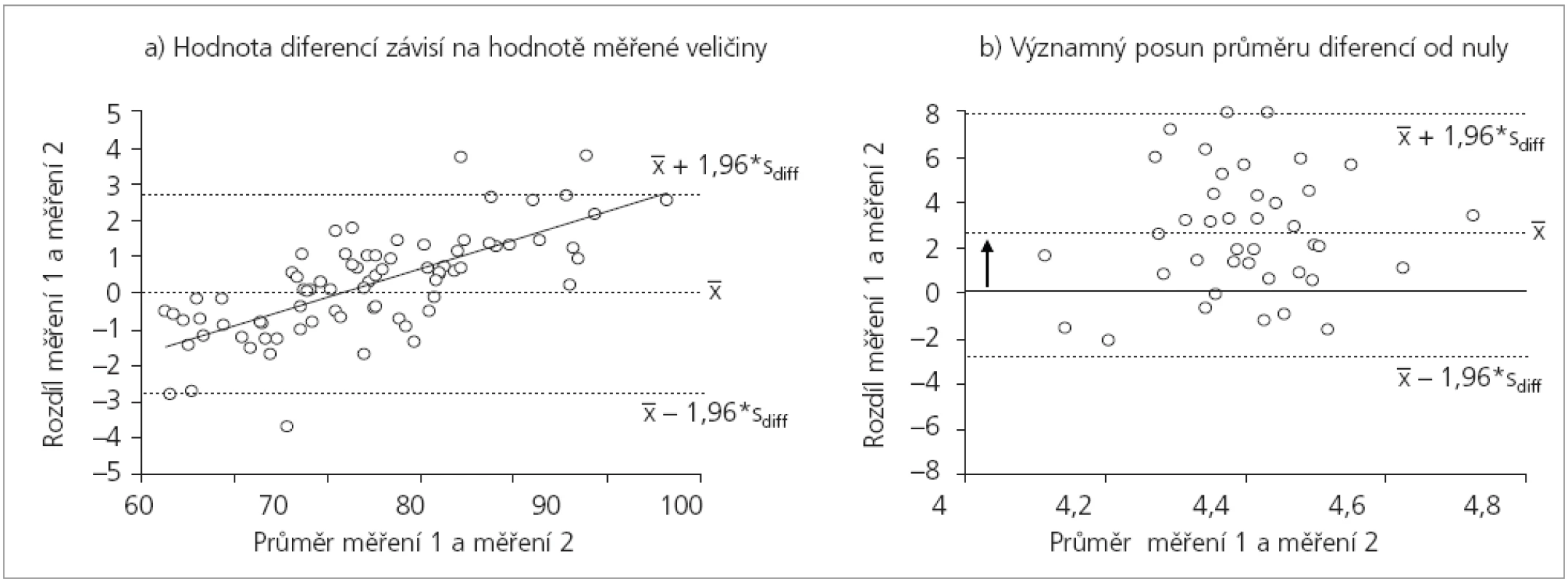
Hodnocení opakovatelnosti a reprodukovatelnosti musí pracovat s kvantitativními rozdíly opakovaných měření. Nelze je nahradit jinými mírami jako například korelací mezi opakovanými měřeními. Sám fakt, že opakovaná měření mezi sebou významně korelují ještě neříká nic o jejich skutečné shodě. Opakovaná měření mohou na dvourozměrném grafu vytvářet téměř ideální přímku, tato ale může mít různý sklon a může maskovat systematické nadhodnocování nebo podhodnocování některého z experimentátorů. Proto je korelace jako míra opakovatelnosti nebo reprodukovatelnosti zcela nepřijatelná. Nízký informační potenciál korelačního grafu je patrný i na obrázku 1b. Obr. 2a-b dále zobrazují situace, kdy hodnocení indikuje rozdílný rozsah diferencí mezi opakovanými měřeními. Korelační koeficient mezi měřeními by tyto rozdíly vůbec neodhalil.
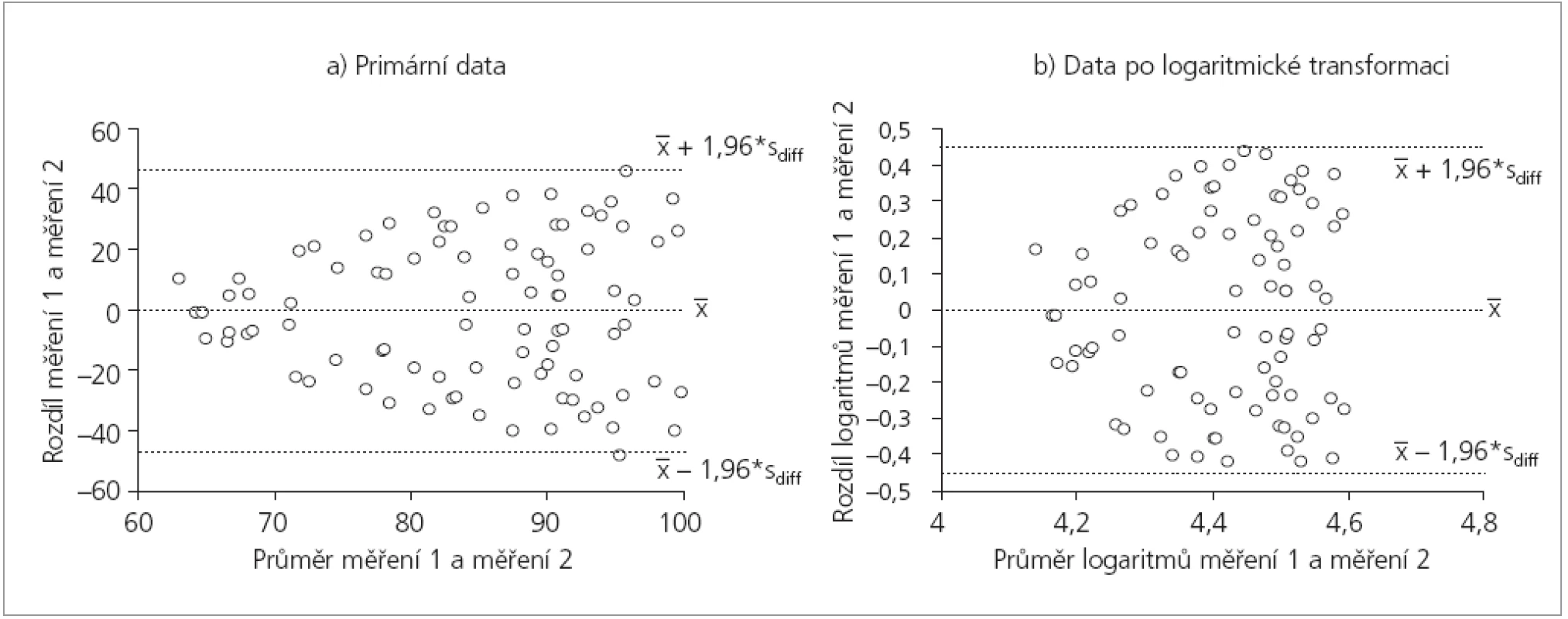
Z grafů dle práce Bland a Altman (1986) lze vyčíst i další skutečnosti, které dokumentují příklady na obr. 3–4:
- Zjistíme-li, že diference opakovaných měření (osa Y) souvisí s hodnotou měřené veličiny (osa X), musíme tuto skutečnost prošetřit. Na obrázku 3 je znázorněna situace, kdy diference narůstají s rostoucí hodnotou znaku. Zde téměř vždy pomůže logaritmická transformace (obr. 3a a 3b). Obecně jakýkoli vztah mezi hodnotami diferencí a hodnotami měřeného znaku indikuje narušení předpokladu normality rozložení a musí být prověřen.
- Diference opakovaných měření mohou vykazovat systematický rostoucí nebo klesající trend s rostoucí hodnotou měřeného znaku (obr. 4a) anebo se mohou v průměru významně odchylovat od nuly (obr. 4b). Obě situace ukazují na vážné systematické zkreslení opakovaných měření a je nutné prošetřit jejich příčinu v primárních datech.
Jak vidno, k testování opakovatelnosti a reprodukovatelnosti máme k dispozici jednoduché početní i grafické nástroje. Zvídavé čtenáře jistě napadne, že všechny zde uvedené příklady pracovaly pouze se dvěma opakovanými měřeními. Jak ale postupovat v případě, kdy je opakovaných měření více? Pokud máme data opakovaných měření pro každého ze zapojených experimentátorů, je nutné korigovat odhad rozptylu diferencí. Hodnocení není ani v těchto případech nijak složité, ale výklad překračuje plánovaný rozsah tohoto dílu. U více než dvou opakovaných měření dále přichází ke slovu analýza rozptylu, kterou se budeme zabývat v některém z příštích dílů seriálu. Nicméně i u takových dat můžeme plně uplatnit zde prezentované výpočty a grafy navržené Blandem a Altmanem. O významu jejich práce z roku 1986 svědčí i fakt, že dosáhla téměř 10 000 citačních ohlasů. Jednoduchý a velmi chytrý nápad tak evidentně pomohl tisícům vědeckých prací. Věříme, že si uvedené grafy oblíbíte i vy a testy opakovatelnosti přestanou být vaším problémem.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz,
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Zdroje
1. Barek J et al. Metrologická terminologie v chemii. Chem Listy 94, 439 – 444 (2000).
2. Bland JM, Altman DG (1986) Statistical method for assessing agreement between two methods of clinical measurement. The Lancet, i, 307-310.
3. Bland JM, Altman DG (1999) Measuring agreement in method comparison studies. Statistical Methods in Medical Research, 8, 135-160.
4. Dewitte K, Fierens C, Stöckl D, LM Thienpont (2002) Application of the Bland-Altman plot for interpretation of method-comparison studies: a critical investigation of its practice. Clinical Chemistry, 48, 799-801.
5. BSI (1975). British Standards Institution. Precision of test methods 1: Guide for the determination and reproducibility for a standard test method (BS 597, Part 1). London: BSI (1975).
Štítky
Dětská neurologie Neurochirurgie NeurologieČlánek vyšel v časopise
Česká a slovenská neurologie a neurochirurgie

2008 Číslo 1
Nejčtenější v tomto čísle
- Bezpečnosť MRI vyšetrenia u pacientov s kovovými implantátmi a implantovanými prístrojmi
- Difuzní gliomy mozkového kmene u dětí. Noční můra dětského onkologa.
- Myasténia gravis
- Klinické využití protilátek u roztroušené sklerózy
