Analýza dat v neurologii. II.
Frekvenční analýza jako první vhled do dat
Autoři:
Ladislav Dušek; Tomáš Pavlík; Jana Koptíková
Působiště autorů:
Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise:
Cesk Slov Neurol N 2007; 70/103(2): 214-217
Kategorie:
Okénko statistika
V předchozím díle tohoto seriálu jsme definovali typy dat a uvedli jsme, že se liší informační hodnotou a použitelnými sumárními statistikami. S postupně rostoucí informační hodnotou dat nominálních, ordinálních, intervalových až poměrových jsme pozorovali větší volnost v aplikovatelných matematických operacích a ve formě vyjádření naměřených hodnot. Jsme si vědomi, že takový teoretický výklad může v čtenáři vyvolat dojem, že sumární statistika je složitý problém. Zopakujme si proto znovu, co je základním cílem statistické sumarizace dat („summary statistics“):
- zpřehlednit primární data, nejlépe ve vhodných grafech
- popsat, jaké jsme naměřili hodnoty
- zachytit případné odlehlé a extrémní body nebo nečekané, nelogické hodnoty
- vypočítat vhodné sumární statistiky, které budou primární data dále nahrazovat (zastupovat) při prezentaci, srovnáních apod.
Jak vidno, statistickou sumarizaci děláme hlavně proto, že chceme do dat vidět. Nikdo pouhým pohledem neodečte potřebné informace ze souboru např. 10 parametrů měřených u 100 pacientů. Potřebujeme grafy a zástupné statistiky, abychom mohli o datech vůbec komunikovat a přemýšlet. Náš problém vyplývá ze skutečnosti, že v biologii a medicíně zkoumáme vzájemně odlišné (rozmanité, variabilní) jedince nebo subjekty. Vždy musíme naměřit větší počet opakování, abychom se dobrali výsledku, který jde rozumně zobecnit. Z jednoho měření můžeme maximálně usuzovat na vlastnost jednoho pacienta. Opakovaná měření odlišných jedinců pak vyžadují:
- sumární statistiku středové tendence, jednoduše řečeno středu – tedy číslo, které zastoupí střední, typickou, průměrnou hodnotu
- sumární statistiku disperze neboli variability, která vyjádří odlišnost jedinců zahrnutých do primárních dat
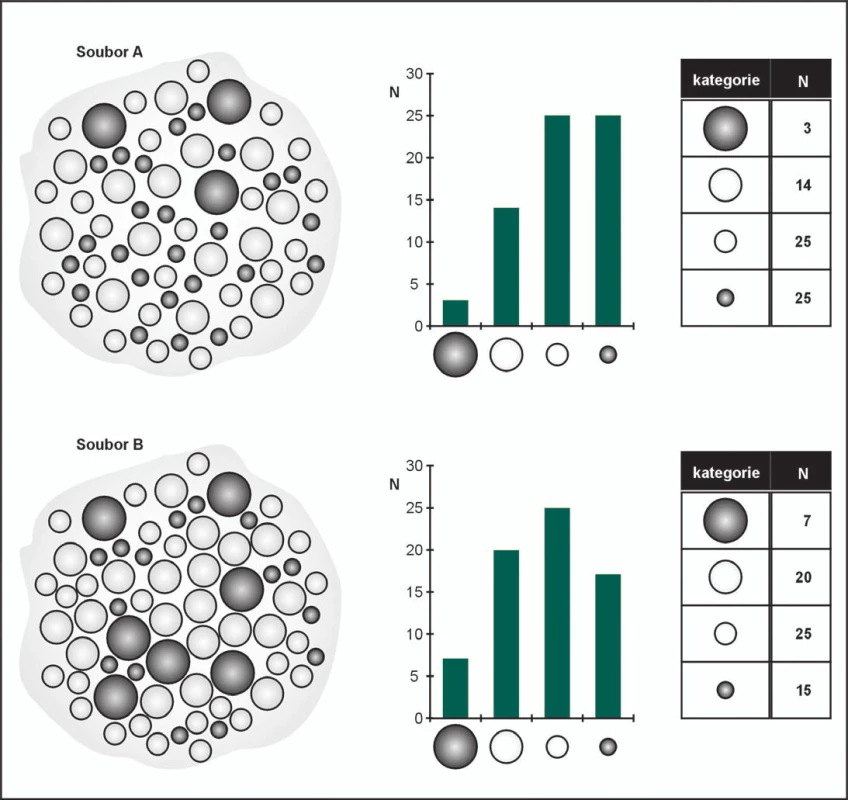
Opusťme teorii a představme si, že stojíme před problémem srozumitelně prezentovat soubor s hodnotami znaku X u dvou skupin pacientů. Na samotném počátku i těch nejsložitějších analýz stojí velmi jednoduchá úvaha - musíme si totiž uvědomit, co měříme (tedy jaké parametry a jakých hodnot mohou nabývat) a jak často tyto potenciálně možné hodnoty skutečně ve výběrovém souboru nastaly. Hovoříme o frekvenční analýze dat, neboť určujeme absolutní četnost (frekvenci) (n) nebo relativní četnost (p, může být vyjadřována jako desetinné číslo nebo procento) možných hodnot. Frekvenční analýzu primárního souboru dat se čtyřmi možnými hodnotami X znázorňuje schematicky obrázek 1. Prostým pohledem do kuliček nahromaděných v souborech A a B nejsme schopni určit téměř žádné parametry ani soubory srovnat. Spočítáním jednotlivých typů kuliček (= možných hodnot měření) získáme frekvenční sloupcový graf nebo frekvenční tabulku, které jednoznačně umožňují:
- určení výskytu libovolné hodnoty, včetně nejčastějších a nejméně častých hodnot
- určení nelogických nebo nečekaných hodnot
- určení „tvaru“ sloupcového grafu (symetrický, asymetrický, ….)
- vzájemné porovnání souborů a určení rozdílů
Jistě jste z obrázku 1 potěšeni, tak jak musel být potěšen i člověk, kterého někdy v minulosti poprvé napadlo nejen dávat věci na hromadu, ale přitom také počítat, kolik kterých věcí je. Myšlenka primitivní a zároveň geniální, neboť vede ke zcela nové kvalitě vnímání skutečnosti. Při pohledu na obrázek 1 se jistě už nikomu nebude chtít trávit čas nad hromadou kuliček, všichni budou chtít frekvenční graf nebo tabulku. Během okamžiku tak srovnáme hodnoty ne ve dvou, ale klidně v deseti i více souborech.
Na obrázku 1 jsme se tak přiblížili k pojmu výběrové rozdělení naměřených hodnot („sample distribution“), jehož znalostí je v učebnicích podmiňována vhodná volba sumární statistiky. Složité tvrzení, jehož význam je ale zásadní. Pouze obtížně bychom rozhodli o správné sumarizaci hodnot, když neznáme, jaké hodnoty a v jaké četnosti v souboru máme. Průzkum výběrového rozdělení začíná frekvenční analýzou tak, jak byla popsána na obrázku 1. Rozdělení hodnot lze nejlépe vysvětlit jako graf, kde jsou na ose X numericky vyneseny naměřené hodnoty a osa Y vyjadřuje absolutní nebo relativní četnost výskytu jednotlivých hodnot nebo jejich kategorií. V podstatě vyjadřujeme, jak jsou hodnoty znaku „rozděleny (rozloženy)“ na ose X. Uspořádáním hodnot na numerické ose X a vynesením četnosti na ose Y vzniká typický obrázek, který vizuálně získává určitý tvar.
Obrázek 2 rozšiřuje metodické schéma z obrázku 1 a uvádí takový průzkum rozdělení hodnot nejen pro diskrétní (nominální, ordinální) znak, ale i pro znak spojitý, který může nabývat libovolných hodnot z určeného číselného intervalu. Je samozřejmé, že grafické zviditelnění tvaru rozdělení se u diskrétních a spojitých znaků musí lišit. Spojitá čísla vzhledem ke své schopnosti „zcela pokrýt“ osu X neumožňují přímé sledování výskytu jednotlivých hodnot, protože každá unikátní hodnota se v souboru pravděpodobně vyskytne jen jednou. Nejprve je nutné rozdělení čísel do kategorií (intervalů) a následné vyhodnocení výskytu těchto kategorií. Standardním grafickým vyjádřením frekvenční analýzy spojitých dat je histogram četností (obr. 2). Osa Y histogramu vyjadřuje intervalovou hustotu četnosti (tj. četnost na jednotku šířky intervalu). Je-li histogram konstruován z dostatečného počtu hodnot, pak tvar této funkce odpovídá skutečné charakteristice jejich rozdělení. Z tvaru rozdělení spojitých znaků jsme opět schopni odečíst, které hodnoty jsou běžné (nejvíce pravděpodobné) a které naopak vzácné až extrémní.
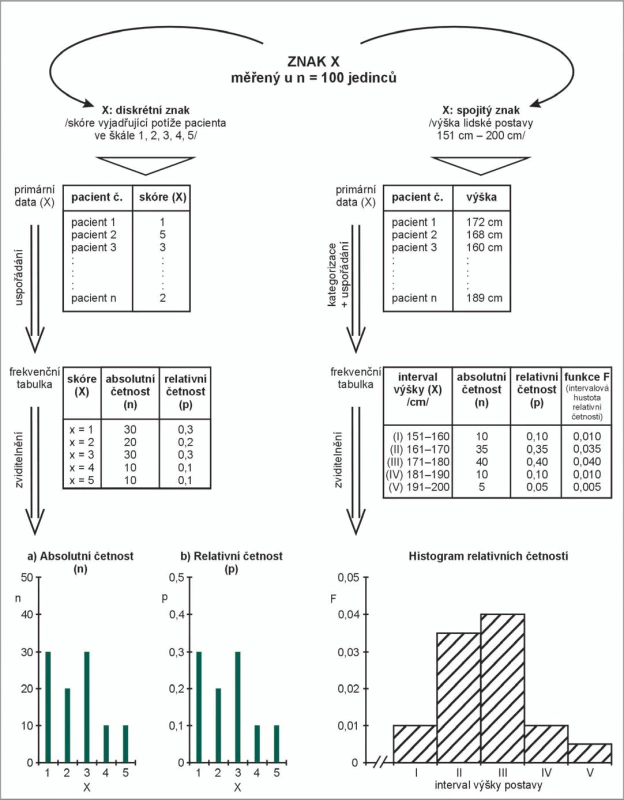
Intervaly osy X mohou být i různě široké, a tak vyjadřovat různá pásma např. patologických a normálních hodnot. Osa Y histogramu může být počítána z absolutní četnosti v intervalech (absolute frequency histogram) nebo z relativní četnosti (relative frequency histogram), aniž by se tím měnil tvar zobrazeného rozložení. Tvar grafu však ovlivní volba počtu intervalů. Je-li histogram založen na stejně širokých intervalech, pak mohou být přímo na osu Y vynášeny četnosti hodnot, tj. bez dělení na jednotku šířky intervalu. Osa Y potom ovšem číselně nepředstavuje intervalovou hustotu četnosti. Tento postup je ale nepřijatelný pro histogramy s různě širokými intervaly hodnot. Zde je vztažení údaje o četnosti na jednotku šířky intervalů podmínkou srovnatelnosti různých histogramů. Histogram totiž není sloupcový graf! Osa Y vyjadřuje pravděpodobnost výskytu hodnot v daných intervalech, nikoli pouze jejich počty.
V tomto díle jsme uvedli frekvenční analýzu jako první a nezbytný krok analýzy souborů s opakovaným měřením více jedinců. Vysvětlili jsme si postup a výstupy frekvenční analýzy u diskrétních a spojitých dat, včetně pojmu výběrové rozdělení hodnot. Tak jako v první části, pokusíme se i zde skončit „moudrým“ doporučením. Frekvenční analýza umožňuje v době osobních počítačů velmi pohodlnou a rychlou kontrolu i velkých souborů se stovkami hodnot. Neměla by se tedy nikdy podceňovat, i když je zdánlivě primitivní. I kdyby nic jiného, můžeme tak velmi snadno odhalit číselné překlepy především v desetinných místech. Máte-li uprostřed velkého souboru dat místo správné položky 1,21 zapsáno 121, je jistě lepší na to přijít na počátku práce než na jejím konci. Mějme tedy frekvenční analýzu rádi.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz,
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Štítky
Dětská neurologie Neurochirurgie NeurologieČlánek vyšel v časopise
Česká a slovenská neurologie a neurochirurgie

2007 Číslo 2
Nejčtenější v tomto čísle
- Epilepsie a cyklus spánku a bdění
- Súčasný pohľad na diagnostiku a terapiu afázie
- Komplikace operací z předního přístupu pro degenerativní onemocnění krční páteře
- Zhoršování epileptických záchvatů a epilepsií antiepileptiky - je to možné?
