Analýza dat v neurologii
XLIII. Grafy usnadňující studium zavádějících faktorů v asociačních studiích – I. Kategoriální data
Autoři:
L. Dušek; T. Pavlík; J. Jarkovský
; J. Koptíková
Působiště autorů:
Masarykova univerzita, Brno
; Institut biostatistiky a analýz
Vyšlo v časopise:
Cesk Slov Neurol N 2014; 77/110(1): 125-129
Kategorie:
Okénko statistika
Předchozí díly seriálu otevřely poměrně závažné téma vlivu zavádějících faktorů na vztah „expozice‑ účinek (jev)“, který nejčastěji analyzujeme v asociačních studiích. Zavádějící faktor ve své typické podobě ovlivňuje výskyt sledovaného jevu a při nerovnoměrném výskytu v ramenech studie tak zkresluje výsledek. Předchozí díl seriálu nově definoval jednu z nejkomplikovanějších forem takových interakcí, kdy zavádějící faktor interaguje i se samotnou expozicí. Příkladem je situace, kdy sledovaná domácí léčba nějakého onemocnění (expozice) působí protektivně na výskyt komplikací u pacientů (následek, účinek) s lehkým diabetem, zatímco u těžkých diabetiků je domácí léčba z tohoto pohledu riziková, a působí tedy opačně. Diabetes zde představuje zvláštní formu zavádějícího faktoru, tzv. faktor modifikující účinek (effect modulating factor) – viz díl 42 seriálu. V extrémních případech způsobují různé formy zavádějících faktorů tzv. Simpsonův paradox, kdy analýzy dílčích podsouborů vedou k opačnému výsledku než analýza spojených dat (díly 41 a 42 seriálu).
Je zřejmé, že identifikace zavádějícího faktoru, ať již působí jakkoli, je komplikovaná. Nicméně chceme‑li průkazně publikovat správné výsledky studií, nelze se jí vyhnout. U prospektivních randomizovaných studií je dnes již povinným krokem doložit, že účinek (jev) popisovaný na celém souboru studie platí také na dílčích podsouborech (stratifikovaných např. dle věku, pohlaví, komorbidit apod.). Dobře vedené studie tak usilují o vyvážený design u všech známých zavádějících faktorů, které mají velký potenciál zkreslit výsledky. Vyvážený design (balanced design) znamená, že např. pomocí randomizačního plánu zajistíme, aby se daný faktor vyskytoval se stejnou četností ve skupině experimentální i kontrolní, obecně tedy v ramenech studie. Proto jsou v literatuře zavádějící faktory označovány jako problém observačních studií, zejména retrospektivních, kde nemůžeme výskyt vybraných faktorů kontrolovat předem pomocí randomizace či jiného nástroje. Kontrola potenciálního zkreslení je u těchto studií velmi významná.
V tomto a v následujícím díle doplníme příklady z dílů předchozích ukázkami grafických metod, jež jsou při studiu zavádějících faktorů užitečné. Věříme, že upoutají pozornost zejména lékařů a přírodovědců, kteří často při studiu dat upřednostňují grafickou vizualizaci před výpočty. Grafy sice výpočty nenahradí, mohou ale identifikovat vážná zkreslení a navést analytika na správnou cestu uvažování. Použité příklady jsou inspirovány dvěma publikovanými pracemi, jež čtenářům rovněž doporučujeme: Paik (1985) a Baker a Kramer (2001).
Již v díle 42 jsme uvedli interakční grafy podle M. Paika (1985), které vztahují šanci výskytu sledovaného jevu k hodnotám aplikované expozice. Tento vztah je v jednom grafu vykreslen jak pro celý soubor, tak pro všechny uvažované podsoubory podle daného faktoru. Velikost bodů odráží i velikost strat ve smyslu počtu pozorování, v jednom grafu tudíž můžeme posoudit i jejich váhu, resp. míru vlivu na celkový výsledek. To je zvláště potřebné u studií s nevyváženým designem, protože na celkový výsledek mají logicky větší vliv strata s větším počtem opakování. Aplikaci a interpretaci tohoto typu grafu zde připomíná příklad 1.

Graf v příkladu 1 vykresluje na ose x hodnotu expozice (v nejjednodušším záznamu kódovanou binárně, ano/ ne) a na ose y velikost účinku, resp. odpověď systému (v našem příkladu šanci výskytu sledovaného jevu). Zavádějící faktor slouží jako stratifikační kritérium, podle jeho hodnot se zakreslují úsečky náležející jednotlivým stratům uvnitř grafu. Graf je velmi přehledný i při větším množství strat, nicméně není to jediná možnost, jak zkoumané interakce faktorů znázornit. V roce 2001 navrhli Baker a Kramer jinou formu zobrazení, která kvantitativněji pracuje s hodnotami zavádějícího faktoru. Tento typ grafu byl po nich nazván „Baker – Kramer Plot, BK Plot“. V tomto grafu zůstává na ose y velikost účinku sledované expozice, ale na ose x jsou vyneseny relativní četnosti zkoumaného zavádějícího faktoru, který pro tento typ zobrazení musí být kategorizován do dvou skupin. V původní práci autorů bylo takto použito pohlaví pacientů. Třídicím faktorem úseček uvnitř grafu jsou hodnoty expozice, tedy např. ramena studie s různou léčbou apod.
Přidaná hodnota BK grafů je možnost přímo sledovat vliv hodnot zavádějícího faktoru (osa x) na účinek expozice (osa y). Uvnitř BK grafů pak lze vykreslit i více ramen studie nebo více experimentů dle hodnot expozice. Aplikaci těchto grafů v různých situacích zde přibližují příklady 2– 4.



Příklad 2 je ukázka situace, kdy spojená data dílčích podsouborů ukazují opačný výsledek než dílčí analýzy. Spojení dat je zde nicméně chybné, neboť zanedbává vliv významného stratifikačního faktoru (zde věku), který není v dílčích souborech rovnoměrně rozložen. Při takto nevyváženém designu studie, jenž je příčinou výrazné heterogenity mezi rameny studie, nelze jednoduše tyto podsoubory spojovat. Tato víceméně klasická ukázka Simpsonova paradoxu byla v původní práci Bakera a Kramera vysvětlena pomocí velmi instruktivního číselného příkladu (tab. 1).
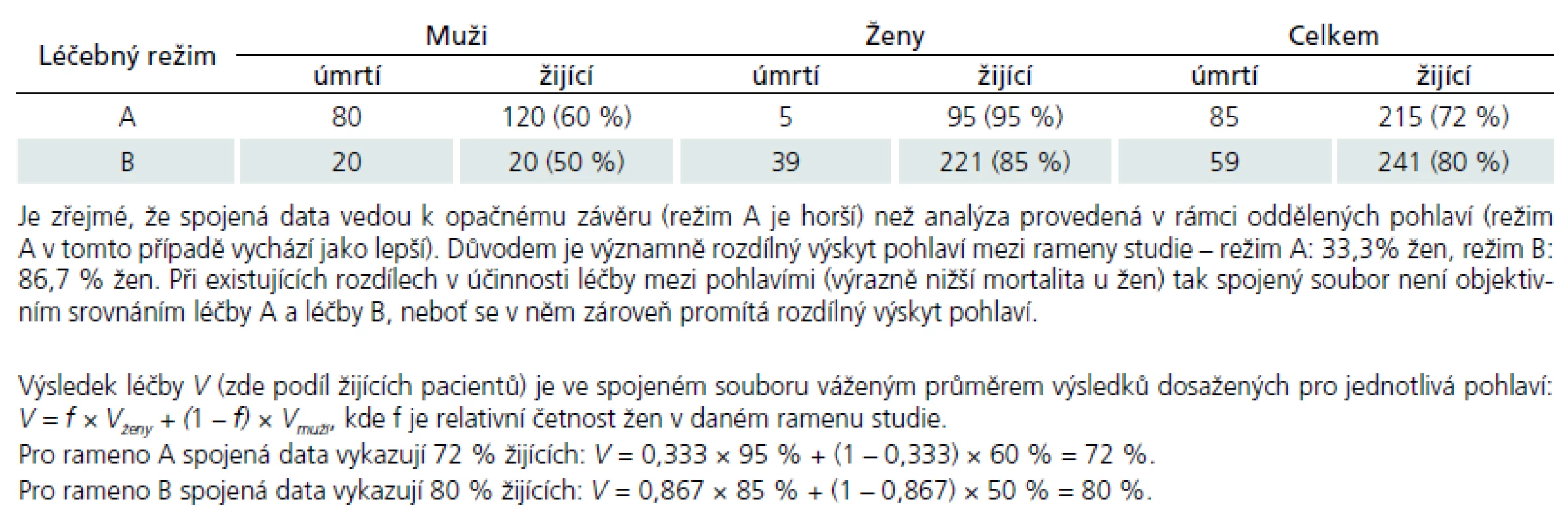
Přiložený příklad 2 dokumentuje podobnou situaci prostřednictvím jiného číselného příkladu a doplňuje výpočet grafem podle metodiky navržené Bakerem a Kramerem.
Příklad 3 doplňuje výklad s pomocí stejné grafické techniky o situaci, kdy zkoumaný zavádějící faktor nemá žádný vliv na účinek léčby, a tudíž jeho různý výskyt ve srovnávaných skupinách pacientů nijak neovlivňuje výsledek. Podsoubory vytvořené na základě úrovní tohoto faktoru lze tak spojit bez rizika zkreslení výsledku. Vraťme se opět k práci Bakera a Kramera, kde autoři tuto situaci opět vysvětlili pomocí číselného příkladu. Tento příklad zde uvádíme v tab. 2.

Poslední příklad 4 ukazuje situaci podobnou příkladu 2, kdy zkoumaný zavádějící faktor ovlivňuje výsledek léčby, a tudíž je nutné kontrolovat jeho výskyt v ramenech studie. Na rozdíl od příkladu 2 na tomto místě ale analyzujeme data pořízená z plánované prospektivní studie, která kontrolovala zastoupení jednotlivých úrovní zavádějícího faktoru, a vedla tak k vyváženému designu a plné srovnatelnosti ramen studie. Baker a Kramer ve své práci tuto situaci dokládají pomocí číselného příkladu, který zde přinášíme v tab. 3.
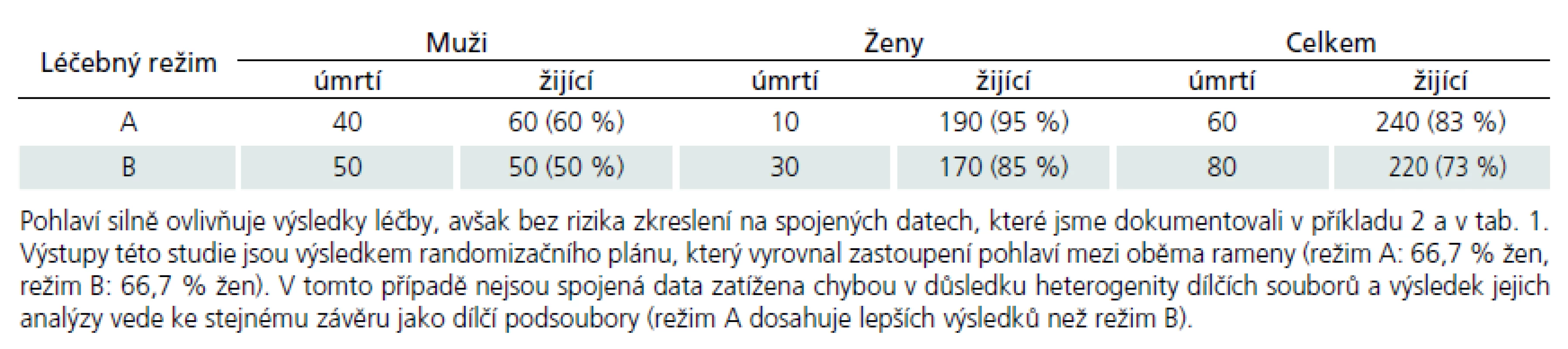
Z grafických zobrazení v příkladech 2– 4 jsou patrné hlavní výhody grafů Bakera a Kramera:
- vynesení hodnot zavádějícího faktoru na osu x nám dává možnost přímo kvantifikovat výsledek expozice pro různé podsoubory (kohorty); nejde tedy jen o doplňující analytické grafy – zároveň je lze využít i pro srovnání kvantitativních výsledků studie,
- v grafu přímo srovnáváme ramena studie, resp. kohorty ovlivněné různou expozicí; tyto grafy tedy mohou sloužit i jako přímá dokumentace výsledků komparativních studií,
- z průběhu úseček v grafu okamžitě odvodíme, zda analyzujeme zavádějící faktor skutečně ovlivňující výsledek studie anebo faktor, jehož vliv je zanedbatelný; různý sklon úseček navíc identifikuje faktor modifikující účinek expozice.
Výhodou grafů dle Bakera a Kramera je snadné využití pro všechny typy asociačních studií a také přehlednost. Na jedné tiskové straně publikace lze takto graficky znázornit vliv mnoha potenciálně zavádějících faktorů formou, která bude pro čtenáře snadno srozumitelná a přehledná. Jediný omezující prvek této techniky je požadavek, aby zkoumaný zavádějící faktor byl binární, dichotomický. Pokud tento požadavek nelze splnit, pak musíme sáhnout po jiných typech grafů – a těmi se budeme zabývat v dalších dílech seriálu.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
MU, Brno
e-mail: dusek@cba.muni.cz
Zdroje
1. Baker SG, Kramer BS. Good for women, good for men, bad for people: Simpson’s paradox and the importance of sex‑ specific analysis in observational studies. J Womens Health Gend Based Med 2001; 109): 867– 872.
2. Paik M. A Graphic Representation of a Three‑ Way Contingency Table: Simpson‘s Paradox and Correlation. Am Stat 1985; 39(1): 53– 54.
3. Rücker G, Schumacher M. Simpson‘s paradox visualized: the example of the rosiglitazone meta‑analysis. BMC Med Res Methodol 2008; 8: 34– 42.
4. Simpson EH. The interpretation of interaction in contingency tables. J Roy Stat Soc B 1951; 13: 238– 241.
Štítky
Dětská neurologie Neurochirurgie NeurologieČlánek vyšel v časopise
Česká a slovenská neurologie a neurochirurgie

2014 Číslo 1
Nejčtenější v tomto čísle
- Mikrochirurgická léčba symptomatických pineálních cyst
- Chirurgická léčba hydrocefalu
- Stiff‑ person syndrom sdružený s myotonickou dystrofií 2. typu – kazuistika
- Mezinárodní standardy pro neurologickou klasifikaci míšního poranění – revize 2013
