Analýza dat v neurologii XVIII.
O t-testu jsme ještě nenapsali vše
Autoři:
L. Dušek; T. Pavlík; J. Koptíková
Působiště autorů:
Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise:
Cesk Slov Neurol N 2009; 72/105(6): 589-596
Kategorie:
Okénko statistika
Nadpis této části seriálu skutečně nelže. Na počátku jsme v 16. díle popsali jednotlivé typy t‑testu, nicméně se zdůrazněním, že jde o parametrický test s předpoklady o výběrovém rozdělení náhodné veličiny. Proto jsme se v minulém díle č. 17 věnovali neparametrickým testům a doporučili jsme je pro situace, kdy si splněním předpokladů pro t‑test nejsme jisti. Stále ale zbývá vysvětlit, jak vůbec o platnosti nebo neplatnosti předpokladů pro t‑test rozhodujeme a jak toto rozhodování ovlivňuje celkový přístup k datům experimentu. I tento postup by měl být řádně podložen a neměl by být výsledkem subjektivní volby analytika.
Spojíme tedy poznatky z předchozích dvou dílů do ucelených postupů, které mají univerzální platnost. A opět zdůrazňujeme, že i v době rozmachu osobních počítačů mají taková schémata smysl. Statistický software samozřejmě provede i složité výpočty, nicméně sám nerozhodne o správné volbě testu pro konkrétní data. Toto „know-how“ náleží výhradně člověku; stroje zde mají k převaze ještě hodně daleko. Čtenáři nabízíme následující shrnující schémata:
- obr. 1 shrnuje postup pro tzv. nezávislé uspořádání experimentu vedoucí k srovnání hodnot sledované veličiny ve dvou nezávislých náhodných výběrech.
- obr. 2 shrnuje postup při srovnání hodnot náhodné veličiny v párově uspořádaném experimentu, kdy mezi oběma srovnávanými výběry existuje souvislost (např. srovnávání sledované proměnné před operací a po ní u téhož pacienta apod.).
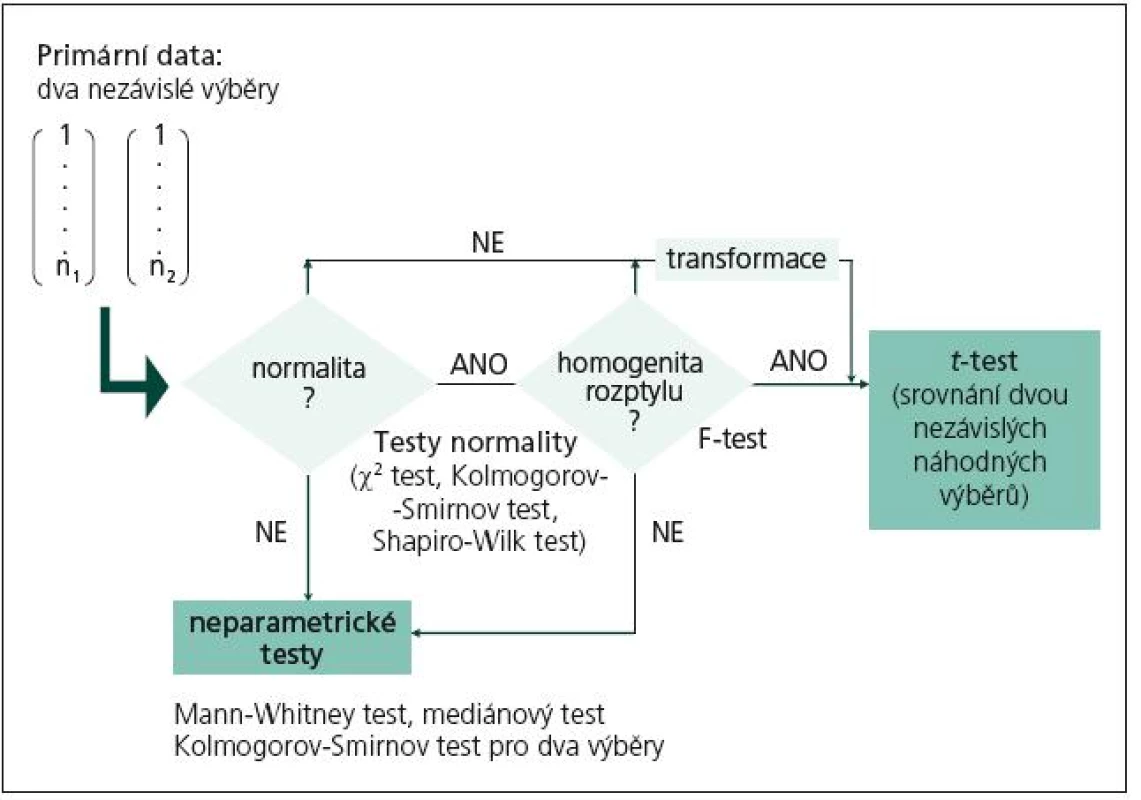
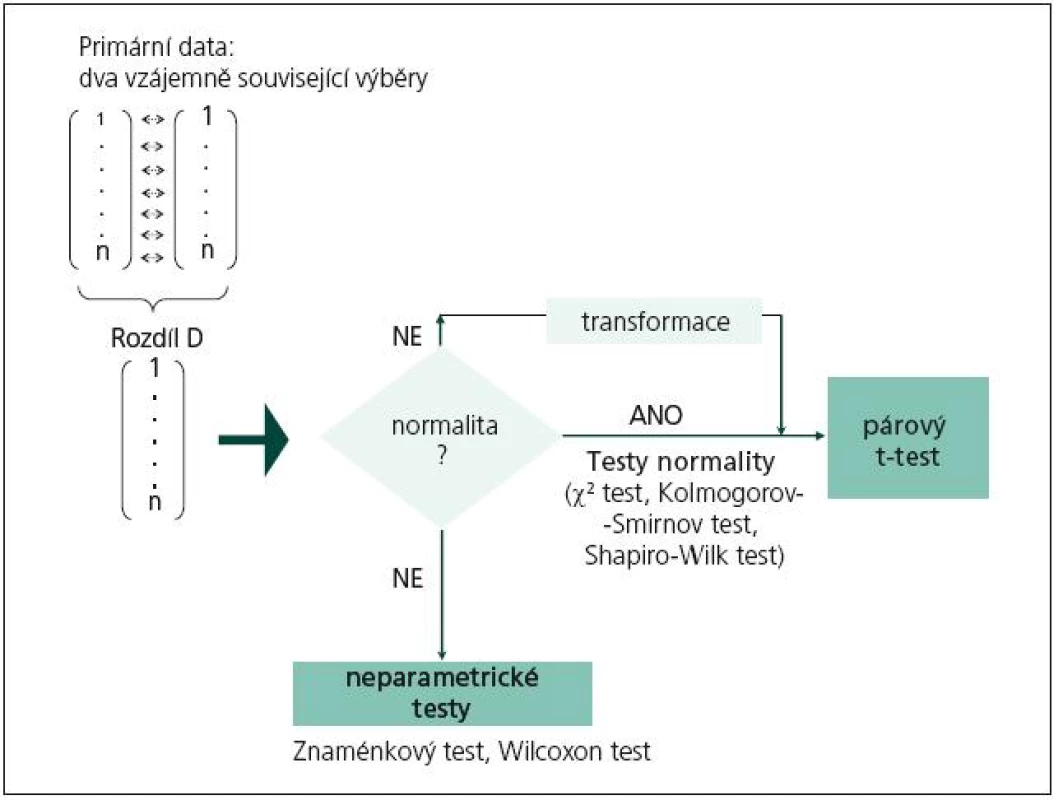
Obr. 1 a 2 se samozřejmě vztahují pouze k situaci, kdy hodnotíme spojitá data, která mohou být podle okolností testována t‑testem i neparametrickými testy. Pokud jsou měřená data nominální nebo ordinální, t‑test nepřipadá v úvahu u žádného experimentálního plánu a přímo přistupujeme k neparametrickým pořadovým testům. Z obou obrázků je patrné, že čtenářům dlužíme výklad k tzv. testům normality, které ověřují nulovou hypotézu normality rozdělení dat. Pokud hypotézu nezamítneme na akceptovatelné hladině významnosti, pak má sledovaná veličina normální rozdělení a můžeme aplikovat parametrické testy. A naopak, pokud je hypotéza zamítnuta, pak data musíme buď transformovat, abychom normality dosáhli (díl 5 seriálu), anebo použijeme neparametrické testy.
Testy normality hrají v rozhodování o testování významnou roli; přitom nepatří k příliš oblíbeným kapitolám biostatistiky. Studenti v nich vidí jakýsi „test pro test“. Tak tomu ale není, tyto testy mohou nést velmi významnou interpretaci i pro biologická a klinická data:
- zamítnutí hypotézy o normalitě rozdělení může indikovat odlehlé, extrémní hodnoty v souboru dat. Test normality může obhájit i případné vyloučení odlehlých bodů;
- pokud o sledované veličině prokazatelně víme, že v cílové populaci nabývá normální rozdělení (např. výška lidské postavy), ale v daném souboru normální rozdělení nepotvrdíme, pak výběr zřejmě není reprezentativní a měl by být prověřen;
- test normality je nezbytný, pokud pracujeme s tzv. z-skóre, tedy se standardizovaným normálním rozdělením (jeho kvantily se mezinárodně označují z). Hodnoty proměnné X (normální rozdělení se střední hodnotou µ a směrodatnou odchylkou σ) se převádějí na hodnoty Z podle vztahu Z = (X – µ)/σ. Následně srovnáváme např. různé skupiny pacientů již přímo v hodnotách Z.
Testy normality jsou podmnožinou testů o rozdělení sledované proměnné. Tak jako normální rozdělení můžeme testovat nulovou hypotézu o jakémkoli modelovém rozdělení, principy i postup jsou stejné. Čtenářům doporučujeme tyto nejčastěji používané testy:
- test dobré shody („Goodness of fit test“). Princip spočívá ve srovnávání pozorovaných četností hodnot v číselných intervalech s teoretickými četnostmi (vypočítanými s distribuční funkce testovaného modelového rozdělení). Jak dokládá příklad 1, konečná statistika testu má Pearsonovo χ2 rozdělení. Tento test můžeme doporučit pouze pro relativně velké soubory dat (n minimálně 30), jinak mohou být pozorované četnosti ve zvolených intervalech příliš malé nebo dokonce nulové.
- Kolmogorov-Smirnovův test (K-S test). Tento test vztahuje empirickou distribuční funkci na získaném náhodném výběru k teoretické distribuční funkci odvozené z testovaného modelového rozdělení. Následně srovnává jejich maximální rozdíl (statistika D) s kritickými hodnotami. Výpočet přibližuje příklad 2.
- Lillieforsův test. Americký profesor statistiky H. Lilliefors upravil původní K-S test specificky pro testy normality, kdy nejdříve odhadujeme průměr a směrodatnou odchylku z naměřených dat. Tato modifikace je při dané velikosti vzorku slabší při prokazování odchylek od normality než původní K-S test.
- Shapiro‑Wilkův test bývá doporučován pro testy normality malých souborů dat. Test vede k výpočtu statistiky W, kterou srovnává s definovanými kritickými hodnotami. Výpočet je popsán v příkladu 3.
- Anderson-Darlingův test srovnává výběrové rozdělení sledované veličiny proti dané (předpokládané) pravděpodobnostní distribuci. Je silnější modifikací K-S testu, nicméně jeho nevýhodou je nutnost přesné specifikace testovaného rozdělení. Kromě normálního rozdělení bývá využíván i pro testy o jiných výběrových rozděleních.




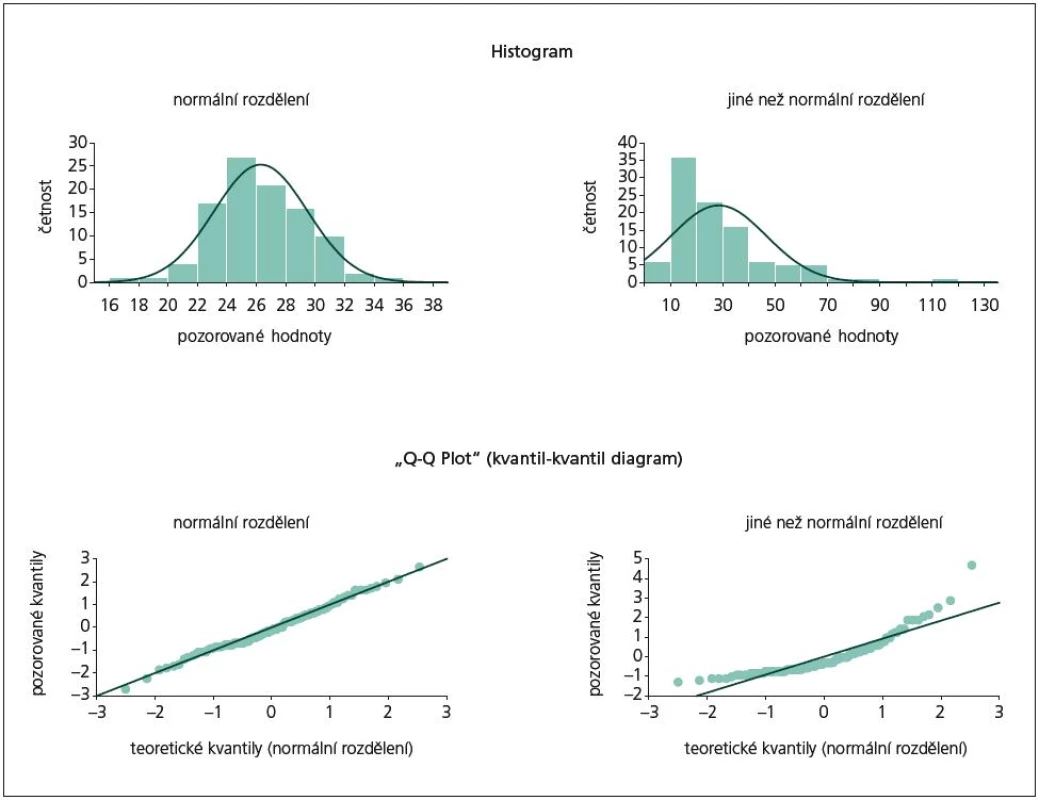
Jak vidno, i u testů normality obdařila statistika lidstvo širokou nabídkou, která ovšem může laického uživatele frustrovat. Věříme, že po přečtení našich doporučení bude pro čtenáře výběr správného testu snadnější. Pro velké vzorky doporučujeme test dobré shody s χ2 statistikou; obecně nelze udělat chybu s K-S testem nebo při menších vzorcích se Shapiro‑Wilkovým testem. A hlavně nikdy nezapomeňme na vizualizaci dat, která je užitečnou kontrolou konečného rozhodnutí. Na obr. 3 nabízíme ukázku dvou možností grafického znázornění. Histogram je jako standard jistě funkční, nicméně pro něj potřebujeme relativně velké vzorky. Naopak tzv. Q-Q plot (kvantil-kvantil diagram) lze vykreslit i pro malý počet naměřených hodnot. Tento graf srovnává kvantilové pozice naměřených hodnot s kvantily předpokládaného, tedy např. normálního rozdělení. V případě 100% shody leží všechny body v grafu na přímce x = y. Výhodou Q-Q diagramu je snadné odhalení odchylek od teoretického předpokladu a také snadná identifikace bodů, které jsou za odchylky odpovědné. Právě z těchto diagramů vychází výpočet statistiky Shapiro‑Wilkova testu.
Zdálo by se, že zde můžeme výklad o testech pro jeden nebo dva výběry důstojně ukončit. Přesto bychom chtěli čtenáře stručně seznámit ještě se dvěma testy, které jsou běžně dostupné v nabídce statistických programů a které mají své místo i ve schématech obr. 1 a 2:
- Kolmogorov-Smirnovovův test pro dva nezávislé výběry („two‑sample K-S test“). Jde o modifikaci výše popsaného testu normality, která srovnává dvě distribuční funkce dvou nezávislých výběrů. Jde tedy o neparametrický test, který stojí v rozhodovacím schématu vedle Mann‑Whitneyho testu (obr. 1). Tento K-S test velmi doporučujeme, zvláště pro výběry o dostatečné velikosti (n > 30). Test totiž prochází celou distribuční funkci a je citlivý vůči všem neshodám, nejen k rozdílům v průměru nebo mediánu. Výpočet ukazuje příklad 4.
- F test srovnávající dva výběrové odhady rozptylu. Tento test využívající statistiku Fisherova rozdělení F testuje nulovou hypotézu rovnosti dvou rozptylů σ12 = σ22. Při zamítnutí této hypotézy neplatí homogenita rozptylu dvou výběrových rozdělení a tato skutečnost brání použití standardního t‑testu. Řešením je buď transformace dat, nebo použití neparametrických testů (obr. 1). Testováním rozptylu se budeme podrobně zabývat v příštím díle seriálu.


Popisem testů normality jsme opět nahlédli do historie matematiky, která zanechala funkční produkty až do dnešní doby. A. N. Kolmogorov (1903–1987) a V. I. Smirnov (1887–1974) byli významní ruští matematici, kteří nesmazatelně přispěli k rozvoji aplikované matematiky. Anderson-Darlingův test byl publikován v roce 1952, Shapiro‑Wilkův test v roce 1965, Lillieforsova modifikace K-S testu o dva roky později. Nicméně stále se objevují nové práce, které možnosti testování normality rozšiřují (např. Farrel a Rogers-Stewart, 2006); častým předmětem zájmu je testování malých výběrových souborů.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Zdroje
1. Anderson TW, Darling DA. Asymptotic theory of certain “goodness- of- fit” criteria based on stochastic processes. Ann Math Statist 1952, 23(2): 193– 212.
2. Lilliefors H. On the Kolmogorov- Smirnov test for normality with mean and variance unknown. Journal of the American Statistical Association 1967; 62: 399– 402.
3. Shapiro SS, Wilk MB. An analysis of variance test for normality (complete samples). Biometrika 1965, 52: 591– 611.
4. Chambers JM, Cleveland WS, Kleiner B, Tukey PA. Graphical Methods for Data Analysis. Chapman and Hall: New York 1983.
5. Farrell PJ, Rogers- Stewart K. Comprehensive study of tests for normality and symmetry: extending the Spiegelhalter test. Journal of Statistical Computation and Simulation 2006; 76(9): 803– 816.
Štítky
Dětská neurologie Neurochirurgie NeurologieČlánek vyšel v časopise
Česká a slovenská neurologie a neurochirurgie

2009 Číslo 6
Nejčtenější v tomto čísle
- Varianty katatonie
- Rettův syndrom
- Neuropatie nervus mentalis jako manifestace systémové malignity
- Syndróm karpálneho tunela
