Analýza dat v neurologii XX.
Statistické testy pro četnosti kategorií – test dobré shody

Je velmi potěšující, že nám jubilejní 20. díl seriálu vyšel právě na test dobré shody. Tento často používaný test patří bez nadsázky mezi několik málo statistických testů, které se staly přímo součástí „know-how“ bio­logů i lékařů. Každý si jistě vzpomene na cvičení z obecné genetiky, kde jsme pomocí tohoto testu ověřovali, zda výskyt homozygotních a heterozygotních jedinců v dceřiných populacích odpovídá Mendelovým zákonům. V tomto díle se pokoušíme přinést praktické ukázky i jiných, taktéž velmi rozšířených, aplikací tohoto testu.

Ačkoli si tedy mnozí spojujeme test dobré shody s ověřováním Mendelových zákonů, sám Mendel jej v době svých pokusů v ruce neměl. Test dobré shody (c² test, chí-kvadrát test) byl publikován až v roce 1900 významným anglickým statistikem Karlem Pearsonem (1857–1936). Proto v anglickém jazyce test najdeme pod heslem Pearson’s chi-square (χ²) test. S osobností Karla Pearsona se v našem seriálu rozhodně nesetkáváme naposledy, minimálně se o něm zmíníme při výkladu o korelačních koeficientech.

Test dobré shody je určen pro srovnání pozorovaných četností jevu (jevů) s četnostmi očekávanými. Máme tedy celkem n jedinců (subjektů), u kterých sledujeme výskyt jednoho jevu (u každého jedince získáváme binární kód: jev nastal/nenastal, 1/0) nebo výskyt více jevů (např. krevní skupina A/B/AB/0). Součet pozorovaných četností jednotlivých jevů v experimentu musí samozřejmě dát dohromady celkovou hodnotu n. Zároveň předpokládáme, že pozorování jednotlivých jedinců jsou vzájemně zcela nezávislá. Očekávané četnosti dopočítáme podle nějakého předem daného klíče (např. předpokládaný poměr sledovaných kategorií dle Mendelových zákonů). Následně ověřujeme nulovou hypotézu, že se očekávané a pozorované četnosti neliší. Formálně můžeme výpočet statistiky testu dobré shody zapsat takto:

Kde:

k je počet jevů (kategorií), které sledujeme

n = k – 1 jsou stupně volnosti pro určení kritické hodnoty testu

E_i je očekávaný počet výskytů jevu i

O_i je pozorovaný počet výskytů jevu i

Je zřejmé, že člen (O_i – E_i)² / E_i je počítán pro každý sledovaný jev i. Výše uvedený vztah má tedy tolik sčítanců, kolik je sledovaných jevů, a pro každý z nich přímo srovnáváme pozorované a očekávané četnosti. Ve výpočtu můžeme mít minimálně dva sčítance (kdy sledujeme pouze, zda nějaká vlastnost nastala, nebo nenastala); maximální počet kategorií není omezen a je označován k.

Pevně věříme, že čtenáři ocení výpočet testu pro jeho jednoduchost. Skutečně málokterý test nabízí tak transparentní vysvětlení principu výpočtu jako právě χ² test. Pozorované a očekávané četnosti jsou pro každý jednotlivý jev jasně odečítány a rozdíl je započítán jako druhá mocnina (O_i – E_i)². Čím větší je rozdíl mezi pozorovanými a očekávanými četnostmi, tím větší je testová statistika, a tedy i pravděpodobnost, že se O a E mezi sebou liší.

Rozdíl pozorovaných a očekávaných četností měříme testovou statistikou, která má chí-kvadrát (χ²) rozdělení. Základním parametrem tohoto rozdělení je již výše uvedené n, tedy tzv. počet stupňů volnosti (n = k – 1, tedy o jednu méně než počet jevů). Testová statistika χ² může tudíž mít nejnižší možný počet stupňů volnosti 1 (pokud sledujeme pouze nastání/nenastání jednoho jevu). Vliv stupňů volnosti na tvar teoretického chí-kvadrát rozdělení ukazuje obr. 1. Všimněme si, že již sama hodnota χ² je druhou mocninou χ, a tedy nabývá pouze kladných hodnot.

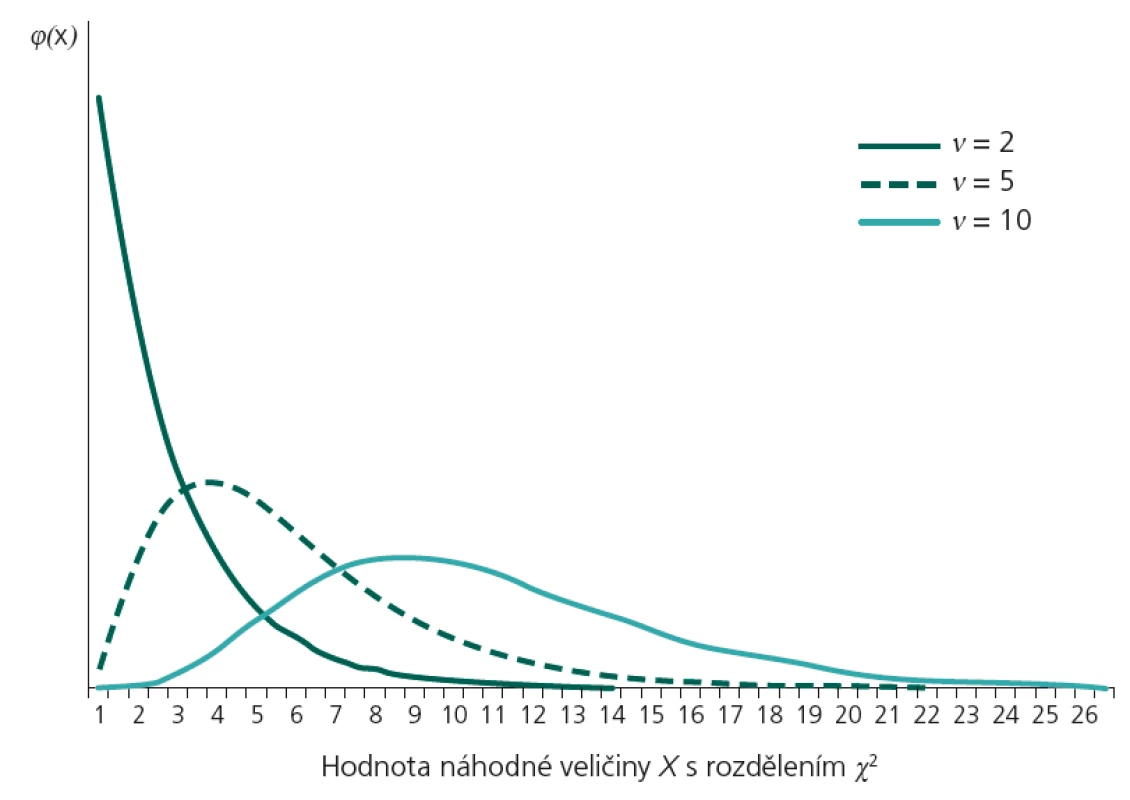
Je zřejmé, že nejnižší možná hodnota testové statistiky χ² je 0, což je případ absolutní shody očekávaných a pozorovaných četností u všech sledovaných jevů. S rostoucími rozdíly mezi O_i a E_i roste také hodnota χ² a ve chvíli, kdy přesáhne kritickou mez χ²_{1 – α} (pro n stupňů volnosti), zamítáme hypotézu shody četností na hladině významnosti α.

Test dobré shody je využitelný pro náhodné veličiny nominální, ordinální i diskrétní; tedy pro všechny typy dat, kde umíme spočítat četnost kategorií. Avšak i spojitá data (třeba výšku postavy) můžeme převést na kategorie, pokud by bylo třeba sledovat výskyt těchto kategorií proti nějakým předpokládaným hodnotám. Tento postup je často využíván v klinické praxi, kdy nepracujeme s primárními hodnotami laboratorních markerů, ale s jejich kategoriemi fyziologickými, rizikovými a patologickými. Jinou modifikací je aplikace testu na výskyt jednoho jevu v časových intervalech. Jednoduše sledujeme, kolikrát nastal určitý jev ve vybraných časových intervalech u kohorty n jedinců (např. počty unikátních pacientů s nějakou komplikací po operaci nebo počty unikátních pacientů s opakovanou hospitalizací po propuštění), a srovnáváme tyto počty s očekávanými četnostmi (dány buď teoreticky, nebo literaturou apod.). Součet pozorovaných a očekávaných četností jednotlivých jevů musí být samozřejmě i v tomto případě shodný a musí se rovnat počtu sledovaných pacientů n. Jednotlivá pozorování pacientů a jejich chování musí být vzájemně nezávislá. Očekávané a pozorované četnosti srovnáváme pro jednotlivé časové intervaly a vztah pro výpočet χ² tedy bude mít k sčítanců, kde k je rovno počtu časových intervalů.

V našem výkladu samozřejmě nemůže chybět ukázka nejjednodušší aplikace testu, kterou zde nabízí klasický hod mincí v příkladu 1. Příklad 2 dále dokumentuje velmi sympatickou vlastnost testové statistiky χ², a sice její aditivitu. Každý jednotlivý zlomek z výše uvedeného vztahu pro test dobré shody je vlastně dílčí komponentou výsledné hodnoty testové statistiky χ². A jelikož tyto komponenty sčítáme, lze jednoduše zjistit, jakým podílem se jednotlivé zlomky (kategorie, jevy) promítají do celkové hodnoty testové statistiky. Tuto vlastnost oceníme především při srovnání očekávaných a pozorovaných četností u více kategorií. Ne všechny kategorie se v reálném výskytu liší stejně od očekávaných četností. Dílčími testy a rozborem hodnoty χ² statistiky (tedy jednotlivých zlomků, které ji v součtu tvoří) můžeme dokonce zjistit, že i při celkovém zamítnutí shody četností se ně­kte­ré kategorie s očekávanými četnostmi prokazatelně shodují a jiné naopak prokazatelně ne. Takové zjištění může mít velký význam. Příklad 2 takto dokumentuje sledování výskytu čtyř typů semen, kdy celkový test dobré shody zamítl shodu pozorovaných a očekávaných četností. Dílčí testy ale odhalily, že za statistickou významnost celkového testu je odpovědná pouze jedna ze čtyř kategorií semen, a pokud je ze sledování vyloučena, pak zbývající tři typy semen se vyskytují přesně ve shodě s očekávanými poměry.

Jinou modifikací testu dobré shody je tzv. test homogenity (shody) binomických rozdělení. Za poněkud složitým názvem se skrývá velmi užitečný postup, který umožňuje ověřit, zda se více vzájemně nezávislých průzkumů (experimentů) liší v relativní četnosti určitého znaku (jevu). Příkladem může být výskyt jevu A v S definovaných kohortách pacientů, které získáme rešerší literatury. Původní autoři ale pracovali s různě velkými soubory, a výstupy tedy nelze bez exaktního ověření jednoduše spojit. Test uvedený v příkladu 3 slouží k ověření následujících hypotéz:

• je výskyt jevu A, resp. jeho relativní četnost, shodná (homogenní) ve všech S dostupných pozorováních, a můžeme tedy pozorování sloučit a odhadnout tak celkovou relativní četnost výskytu jevu?
• pokud relativní četnost jevu A není v dostupných pozorováních shodná, jak se od sebe jednotlivá pozorování liší? Vytvářejí vnitřně homogenní shluky? Jsou mezi nimi viditelně odlehlá pozorování, jejichž vyloučením bychom získali homogenní skupinu?

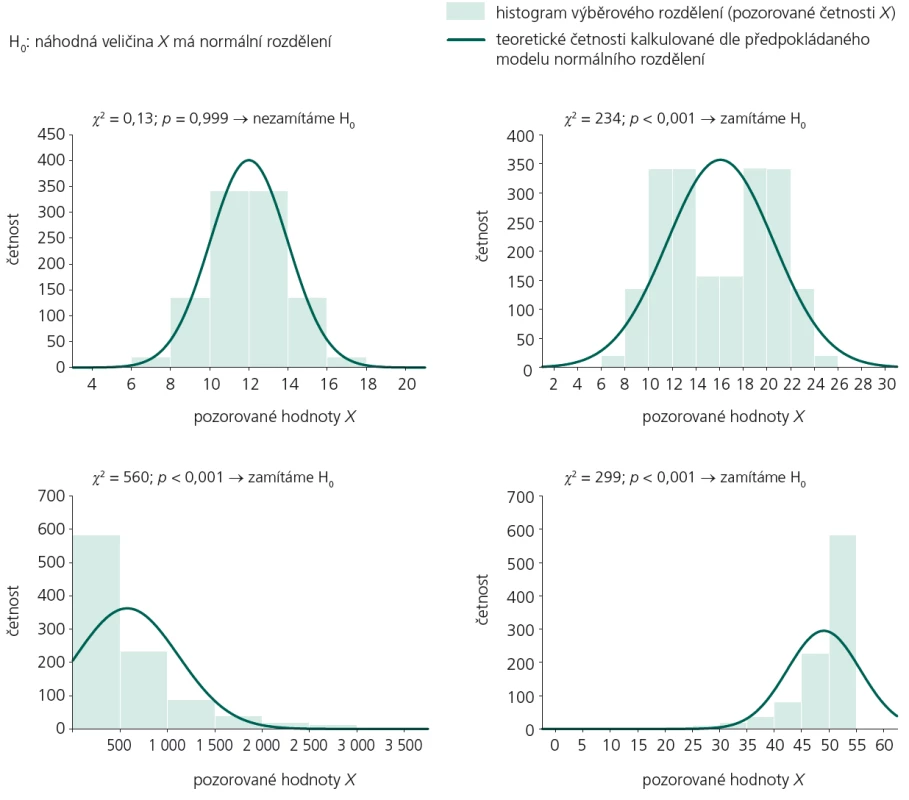
Test dobré shody je velmi často využíván pro ověření předpokladu, že rozdělení pravděpodobnosti náhodné veličiny X je určitého typu, například že odpovídá modelu normálního rozdělení, Poissonova rozdělení apod. Zde se test dobré shody stává metodou matematické statistiky, která ověřuje, zda má náhodná veličina určité, předem dané rozdělení. Vlastní výpočet se nijak zásadně neliší od již uvedeného postupu. Pozorované hodnoty náhodné veličiny X rozdělíme do kategorií, ve kterých zjistíme pozorované četnosti. Očekávané četnosti spočítáme z modelu teoretického rozdělení, které na datech ověřujeme. Jestliže je toto modelové rozdělení dáno předem včetně všech svých parametrů, je počet stupňů volnosti pro χ² test i nadále k – 1. Je‑li ale ně­kte­rý parametr modelového rozdělení neznámý, snižuje se počet stupňů volnosti o jednotku za každý neznámý parametr (neznámé parametry musí být nejprve z naměřených dat odhadnuty a následně využity k výpočtům očekávaných četností podle daného modelu). Test dobré shody je tedy jedním z testů normality rozdělení nebo obecně jedním z tzv. testů goodness-of-fit. Do této rodiny patří i ostatní testy o rozdělení sledované veličiny, které jsme probrali v díle XVIII tohoto seriálu (např. Shapiro‑Wilkův test, Kolmogorov-Smirnovův test). Vybrané příklady aplikace testu dobré shody jako testu normality přibližuje obr. 2.

doc. RNDr. Ladislav Dušek, Dr.

Institut biostatistiky a analýz

Masarykova univerzita, Brno

e-mail: dusek@cba.muni.cz