Analýza dat v neurologii
XIX. Statistické testy pro četnosti kategorií – binomické a Poissonovo rozdělení
Autoři:
L. Dušek; T. Pavlík; J. Koptíková
Působiště autorů:
Masarykova univerzita, Brno
; Institut biostatistiky a analýz
Vyšlo v časopise:
Cesk Slov Neurol N 2010; 73/106(1): 81-84
Kategorie:
Okénko statistika
V minulém díle seriálu jsme ukončili výklad statistických testů zaměřených na hodnocení hypotéz o průměru, mediánu a rozptylu různých rozdělení. Závěrečný přehled v díle XVIII shrnuje parametrické i neparametrické testy a dané téma zdánlivě ukončuje. To ale platí pouze pro spojitá data, u kterých je odhad průměru nebo mediánu standardní statistickou sumarizací. Statistické testy a obecně metody induktivní statistiky můžeme ovšem použít i na všechny typy dat, u kterých je aplikace již probíraných testů (např. t‑testu) nesmyslná. Typickým příkladem je hodnocení četností kategorií nebo četnosti jevu (jevů), pro které potřebujeme jinou sadu testů, specifických pro zde používaná rozdělení.
Připomeňme si, že sledování četností lze modelovat pomocí binomického rozdělení nebo Poissonova rozdělení (díly VIII–IX našeho seriálu).
- Binomické rozdělení popisuje četnost výskytu náhodného jevu v n nezávislých pokusech, v nichž má tento jev stále stejnou pravděpodobnost nastání. Binomické rozdělení tedy popisuje výskyt daného jevu (X) s tím, že na číselné ose x vynášíme, kolikrát tento jev v opakovaných pokusech nastal. Učebnicovým příkladem je hod mincí, kde sledujeme, zda a kolikrát padne líc. Hodíme‑li celkem pětkrát (n = 5), pak líc nemusí nutně padnout ani jednou a nejvíce může padnout právě pětkrát. Na ose x budou tedy diskrétní hodnoty 0, 1, 2, 3, 4 a 5 a pravděpodobnost, že nastane konkrétní hodnota, můžeme zjistit pomocí binomického rozdělení, pokud jsou splněny jeho předpoklady. Jednotlivé hody mincí musí být vzájemně zcela nezávislé a pravděpodobnost nastání sledovaného jevu se v opakovaných pokusech nesmí měnit. U běžné mince v běžných podmínkách je tato pravděpodobnost 0,5 a obecně ji označujeme p, při popisu cílové populace potom π. Hodnota π je tak parametrem binomického rozdělení a určuje pravděpodobnost nastání jevu v jednotlivých experimentech. Ty musí být nastaveny tak, aby byla možná již jen jedna další možnost, tedy jev opačný nastávající s pravděpodobností 1 – π.
- Poissonovo rozdělení je modelem pro výskyt jevů, které se náhodně vyskytují v čase nebo v prostoru s neměnnou pravděpodobností. Počítáme‑li např. mutované kolonie bakterií na Petriho misce, předpokládáme, že pravděpodobnost mutace každé jednotlivé bakterie v průběhu experimentu je stejná a výskyt mutací je zcela náhodný. Jsou‑li splněny tyto předpoklady, můžeme pomocí Poissonova rozdělení modelovat výskyt i častých jevů, ačkoli učebnicovou aplikací je sledování jevů vzácných. Cílem hodnocení je odhad střední hodnoty počtu jevů (sledovaných kategorií) na danou experimentální jednotku (časový úsek, plochu apod.). V Poissonově rozdělení tuto střední hodnotu počtu jevů X označujeme jako λ. Parametr λ je jediným parametrem tohoto rozdělení.
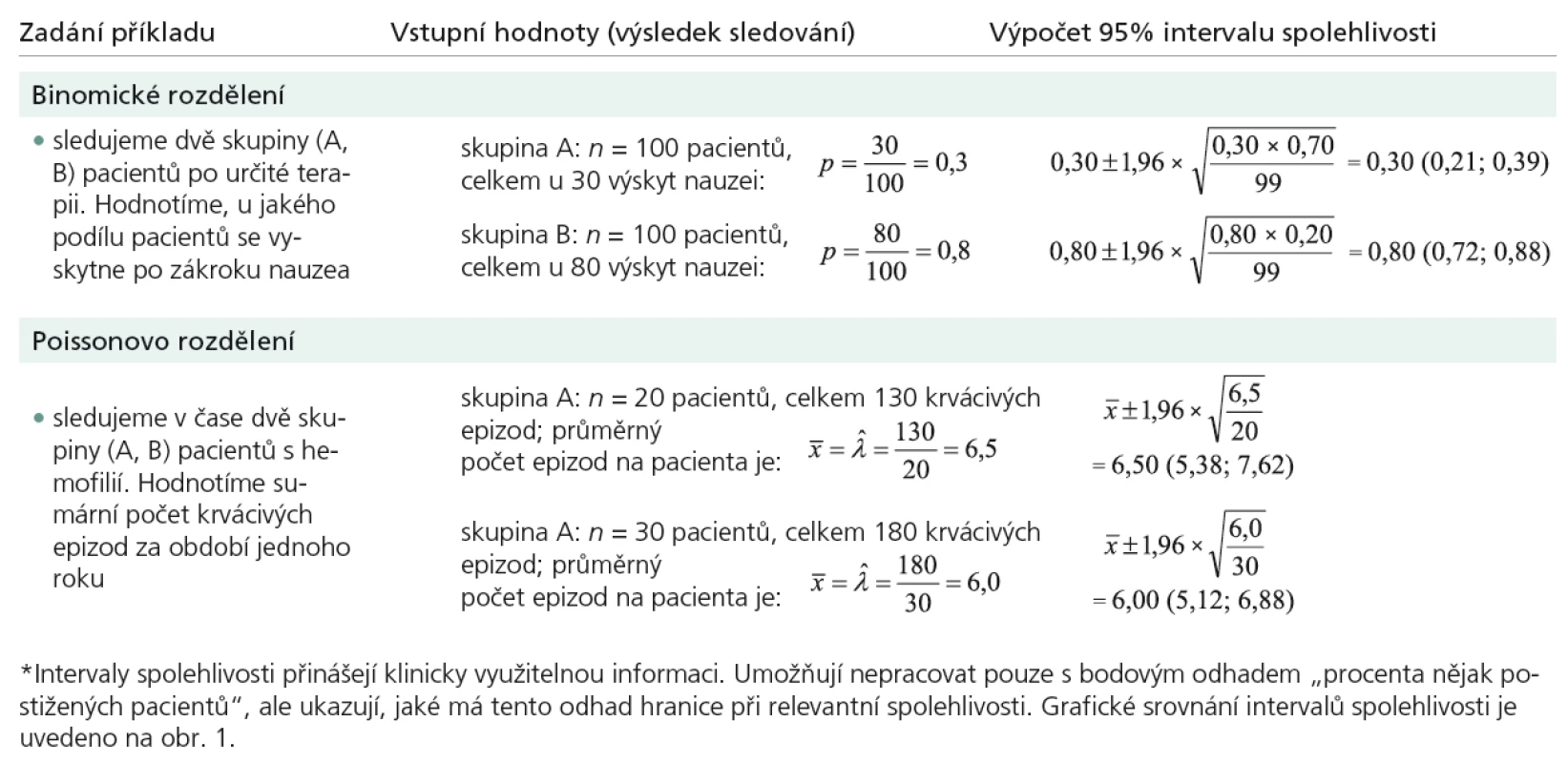
Výše uvedené připomenutí definic se možná jeví jako příliš matematické a plné symbolů. Přesto jde o běžné modely, které mají v hodnocení klinických dat velmi významné místo. Uveďme dva příklady, které mluví samy za sebe: hodnocení podílu pacientů, kteří dosáhnou po terapii určité léčebné odpovědi, nebo sledování výskytu časných nebo pozdních komplikací po léčbě v daných časových intervalech. Úkol srovnat statisticky dvě skupiny pacientů v podílu dosažené léčebné odpovědi je jistě smysluplný a potřebujeme pro něj vhodný statistický test. Avšak všechny testy, které jsme dosud prošli, jsou zde nevhodné, neboť jsou definovány pro jiná rozdělení sledované veličiny. Samotný princip hodnocení nicméně zůstává stejný. Známe‑li tedy příslušné postupy, není problém je na počty četností správně aplikovat. Tab. 1 shrnuje daný problém v termínech, které odpovídají například již probranému hodnocení aritmetického průměru.

V následující části kapitoly přiblížíme čtenářům hlavní postupy těchto hodnocení. Pro laického hodnotitele totiž opět může být kamenem úrazu nalezení správného vztahu nebo postupu výpočtu. I renomované softwarové produkty často kapitoly tzv. frekvenční statistiky umísťují v jiných modulech než např. testy o aritmetickém průměru; uživatel tedy musí vědět, co chce hledat a proč. Testy o parametru Poissonova rozdělení bývají mnohdy dokonce ignorovány. Nevnímejme tedy níže uvedené vztahy jako nutné zlo, ale jako instruktivní nástroj pro realizaci velmi potřebných výpočtů.
Výpočet intervalu spolehlivosti pro parametr π binomického rozdělení
Výpočet s aproximací na normální rozdělení
Kde p je bodový odhad π, n velikost vzorku a z1–α/2 kvantil normálního rozdělení pro požadovanou šířku intervalu spolehlivosti (např. 1,96 pro 95% interval spolehlivosti). Aproximaci na normální rozdělení můžeme využít u výběrů většího rozsahu, kde platí np > 10 a n(1 – p) > 10. U menších výběrů nelze tento výpočet využít.
Výpočet bez aproximace na normální rozdělení (asymetrický interval spolehlivosti)
Pro spodní hranici intervalu:
se stupni volnosti F rozdělení
Pro horní hranici intervalu:
se stupni volnosti F rozdělení
Kde r značí počet nastání jevu ve vzorku o velikosti n a F1-α/2 ν1,ν2 kvantil F rozdělení pro požadovanou šířku intervalu spolehlivosti se stupni volnosti ν1,ν2. Rozdělení F je Fisher-Snedecorovo rozdělení, pro které lze bez problémů nalézt kvantily například i v MS Excel, jediné co potřebujeme znát, je počet stupňů volnosti ν1,ν2.
Výpočet intervalu spolehlivosti bez aproximace na normální rozdělení lze doporučit pro vzácnější nebo naopak časté jevy, kde se hodnota π blíží hranici 0 nebo 1.V takovém případě může (zvláště u menších výběrů) výpočet s aproximací na normální rozdělení vést k nesmyslným hranicím intervalu spolehlivosti menším než 0 a větším než 1. Pomoci kvantilů rozdělení F získáme asymetrické intervaly spolehlivosti, které lépe odpovídají realitě. Použití tohoto výpočtu se tedy doporučuje, když očekáváme hodnoty π nižší než 0,2 nebo vyšší než 0,8.
Výpočet intervalu spolehlivosti pro parametr λ Poissonova rozdělení
Výpočet s aproximací na normální rozdělení
Kde x – je průměrný počet výskytů jevu na experimentální jednotku, tedy bodový odhad střední hodnoty výskytu jevu na experimentální jednotku (λ), n počet těchto jednotek a z1–α/2 kvantil normálního rozdělení pro požadovanou šířku intervalu spolehlivosti (např. 1,96 pro 95% interval spolehlivosti).
Výpočet bez aproximace na normální rozdělení (asymetrický interval spolehlivosti)
Pro spodní hranici intervalu:
se stupni volnosti χ2 rozdělení ν1 = 2n
Pro horní hranici intervalu:
se stupni volnosti χ2 rozdělení ν2 = 2n + 2
Kde n je velikost vzorku a χ21-α/2ν1 a χ21-α/2ν2 kvantily χ2 rozdělení pro požadovanou šířku intervalu spolehlivosti se stupni volnosti ν1,ν2. Rozdělení χ2 je Pearsonovo rozdělení, jehož kvantily jsou běžně dostupné např. i v MS Excel.
Výpočet intervalu spolehlivosti bez aproximace na normální rozdělení slouží opět především pro menší výběry a pro situace, kdy je průměrný počet jevů na jednu hodnocenou jednotku velmi malý, až blížící se nule.


Příklady testů hypotéz o parametrech binomického a Poissonova rozdělení
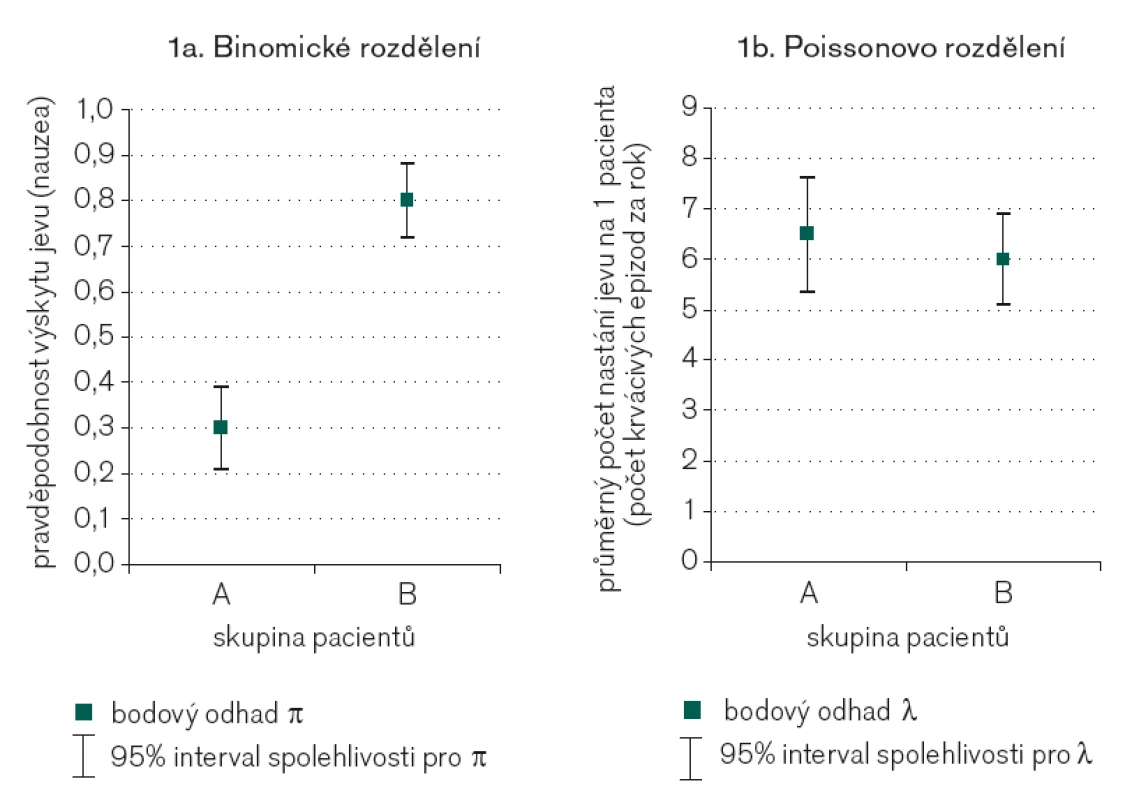
Samotné srovnání intervalů spolehlivosti nemůže nahradit provedení statistického testu srovnávajícího dvě experimentální skupiny. Ukázky výpočtu takových testů pro binomické a Poissonovo rozdělení jsou uvedeny v příkladech 1–2. Jak vidno, hypotézy o výskytu jevů v definované populaci experimentálních jednotek můžeme testovat standardním postupem včetně odečtení statistické významnosti.
Statistické testování četností kategorií může výrazně pomoci i při hodnocení vysloveně kvantitativních parametrů. Například řada výsledků laboratorních vyšetření je obtížně klinicky využitelná ve svém primárním měřítku. Často je výhodnější převést parametry na proměnné typu „ano/ne“ podle toho, zda hodnota překročila již poznanou hranici pro patologické stavy („cut‑off“). Z měření kvantitativního markeru se tímto krokem stává sledování četnosti jevu (hodnota je/není v patologické oblasti).
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Štítky
Dětská neurologie Neurochirurgie NeurologieČlánek vyšel v časopise
Česká a slovenská neurologie a neurochirurgie

2010 Číslo 1
Nejčtenější v tomto čísle
- Mitochondriální encefalomyopatie na podkladě deficitu proteinu Sco2 s obrazem SMA‑like neurogenní svalové atrofie – kazuistiky
- Vyšetření čichu u neurologických onemocnění pomocí Testu parfémovaných fixů
- Kongenitální myastenické syndromy – kazuistiky
- Evokované odpovědi a elektromyografie v intraoperační monitoraci v neurochirurgii








